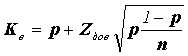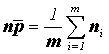Пример 3.1.
Необходимо найти объем мгновенной выборки n и приемочное число Ас, если заданы следующие величины:
— приемочный уровень дефектности р0=0,025;
— браковочный уровень дефектности р1=0,15;
— риск незамеченной разладки ?=0,05;
— риск излишней наладки ?=0,20.
Вычислим величину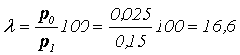 
. Из табл. 3.2 для указанных значений ?, ?, ? определяем приемочное число Ас=1,0. Из табл. 3.3 извлекаем величину w=0,82, которая соответствует найденному значению Ас и ? = 0,20. Теперь можно вычислить объем мгновенной выборки:
.
Таблица 3.3
Значения w при различных значениях риска излишней наладки ?
|
Ас |
? |
Ас |
? |
Ас |
? |
||||||
|
0,05 |
0,10 |
0,20 |
0,05 |
0,10 |
0,20 |
0,05 |
0,10 |
0,20 |
|||
|
0 |
0,05 |
0,11 |
0,22 |
10 |
6,2 |
7,0 |
8,2 |
20 |
14 |
15 |
17 |
|
1 |
0,36 |
0,50 |
0,82 |
11 |
6,9 |
7,8 |
9,0 |
22 |
16 |
17 |
19 |
|
2 |
0,82 |
1,1 |
1,5 |
12 |
7,7 |
8,6 |
9,9 |
24 |
17 |
19 |
21 |
|
3 |
1,4 |
1,7 |
2,3 |
13 |
8,4 |
9,5 |
11 |
26 |
19 |
21 |
23 |
|
4 |
2,0 |
2,4 |
3,1 |
14 |
9,2 |
10 |
12 |
28 |
21 |
22 |
24 |
|
5 |
2,6 |
3,2 |
3,9 |
15 |
10 |
11 |
12 |
30 |
22 |
24 |
26 |
|
6 |
3,3 |
3,9 |
4,7 |
16 |
11 |
12 |
13 |
35 |
27 |
29 |
31 |
|
7 |
4,0 |
4,7 |
5,6 |
17 |
12 |
13 |
14 |
40 |
31 |
33 |
36 |
|
8 |
4,7 |
5,4 |
6,5 |
18 |
12 |
14 |
15 |
45 |
35 |
38 |
40 |
|
9 |
5,4 |
6,2 |
7,3 |
19 |
13 |
15 |
16 |
50 |
40 |
42 |
45 |
Границы регулирования для р-карт вычисляются следующим образом:
; 
, (3.4)
где р — это доля дефектности при налаженном ТП. Для найденных таким образом границ регулирования при заданном значении р1, риск незамеченной разладки ? будет равен: 
, где к — это ближайшее целое к величине 
.
Хотелось бы отметить, что для практического применения важна только верхняя граница регулирования, нарушение же нижней границы регулирования говорит о том, что характеристики ТП значительно лучше тех, которые были заложены при формировании плана контроля. В этом случае рекомендуется сформировать новый план контроля, соответствующий реальным характеристикам ТП.
Иногда объем мгновенной выборки n не является постоянной величиной. В этом случае для каждого значения n необходимо заново найти границы регулирования. Пример такой р — карты представлен на рис. 3.1. Значения верхней границы регулирования вычислены с помощью выражения (3.4). Здесь n поочередно принимает значения 100, 150,120, 100, 80, 90, 90, 60 при р=0,1.
Рис.3.1. Верхняя граница регулирования р — карты для случая переменного n.
При использовании р-карты через установленные промежутки времени (или через некоторое количество изготовленных деталей) извлекаются выборки некоторого объема ni (не обязательно одинакового), подсчитывается количество дефектных единиц ni,d и вычисляется их доля от общего объема выборки: 
. Полученное значение в виде точки наносят на карту. Если при этом хотя бы одна точка пересечет верхнюю границу регулирования, то ТП признается разлаженным.
В ряде случаев вместо р-карты используют так называемую стабилизированную р-карту, или как ее еще называют t-карту. В этом случае вычисляют величину: 
, где 
. Границы регулирования в этом случае будут: Кв=Zдов, Кн=-Zдов. В остальном использование t-карты является таким же, как и р-карты.
Достоинством t-карт является то, что границы регулирования можно нанести на бланк не дожидаясь анализа ТП.
При постоянном значении n — объема мгновенной выборки р-карту можно заменить контрольной картой числа дефектных единиц в каждой выборке – np-картой. На бланки таких карт наносят среднюю линию и границы регулирования.
Среднюю линию определяют по формуле:
, (3.5)
где m — число выборок, а ni – объемы выборок.
Границы регулирования:
; 
. (3.6)
При использовании np-карт через установленные промежутки времени (или через установленное количество изготовленных деталей) извлекаются выборки некоторого объема n (n является неизменной величиной), определяют число дефектных единиц продукции и наносят его на карту в виде точки. Если точка располагается выше верхней границы регулирования, то ТП признается разлаженным.
С-карты используются в том случае, если ведется подсчет не числа дефектных изделий, а числа дефектов (на одном изделии, на некотором количестве изделий). Предполагается, что эта величина распределена по закону Пуассона. Это предположение справедливо, если выполняются следующие условия:
— существует несколько независимо действующих причин образования дефектов;
— на практике дефекты встречаются редко.
На бланки С-карт наносят среднюю линию и границы регулирования.
Значение, по которому строят среднюю линию, вычисляют по формуле:
, (3.7)
где Сi— количество дефектов в i-м проверенном изделии (или в i-й группе проверенных изделий).
Положения границ регулирования вычисляют по формулам:
; 
. (3.8)
При использовании С-карты через установленные промежутки времени (или через установленное количество изготовленных деталей) извлекаются выборки некоторого объема n, определяют число дефектов на единицу продукции и наносят его на карту в виде точки. Если нанесенная точка оказывается выше верхней границы регулирования, то ТП признается разлаженным.
