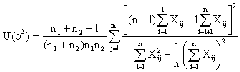Под статистической группировкой принято понимать сведение анализируемых статистических данных в однородные группы на основе существенных для них признаков. Если группа одна это просто однородная статистическая совокупность, а если число групп две или более – мы говорим о группировке. Понятно, что сами группы между собой (одна по отношению к другой) разнородны. Однородность же рассматривается как критерий образования каждой отдельной группы, то есть критерий, на основе которого элементы статистической совокупности объединяются в одну группу.

Формируем таблицу многомерной группировки для проверки критерия U(p­­­²). Сущность критерия заключается в том, что осуществляется последовательный расчет критерия U(p­­­²) для совокупностей l и n-1 и сравнение его с критическим значением при уровне значимости q и m степеней свободы.

для всех ,

где q – желаемый уровень значимости, в противном случае принимается альтернативная гипотеза о существенной неоднородности хотя бы одной строки матрицы (в данном случае величина q равна ). Если выполняется это условие , то совокупность признается однородной (принимается нулевая гипотеза). Если условие не выполняется, то совокупность признается неоднородной (принимается альтернативная гипотеза) и должна быть разбита, по крайней мере, на две группы.

Расчет критерия производится по формуле:

При не выполнении этого критерия исходная матрица разбивается на две группы по строке с U(p²)=max. Каждая из полученных таким образом групп m-мерных наблюдений проверяется на однородность. Если обе группы окажутся однородными, то интервал группировки (граница разбиения исходного пространства) только один, процесс группировки на этом заканчивается. Если же гипотеза об однородности хотя бы для одной группы, то ее нужно разделить на две части по максимальному значению критерия, и каждую из частей в отдельности подвергнуть проверке на однородность. Процедура такого деления неоднородной статистической совокупности продолжается до тех пор, пока не будут образованы все однородные группы.