Ответ 40.1.
Девочка прочла число в перевернутом виде: 98 вместо 86.
Ответ 40. 2.
Поменять местами бумажки с числами 8 и 9, при этом 9 перевернуть как 6. Тогда в каждом столбике будет по 18.
Ответ 41.
23 года. Разность между годами отца и сына равна 23 годам; следовательно, сыну надо иметь 23 года, чтобы отец был вдвое старше его.
Ответ 42.
На первый взгляд кажется, что результаты сложения чисел каждого столбца не должны быть одинаковыми, но, присмотревшись чуть повнимательнее, можно заметить, что если во втором столбце
девять единиц (9 · 1), то соответственно в первом столбце одна девятка (1 · 9); во втором столбце восемь двоек (8 · 2), но в первом — две восьмерки (2 · 8), во втором столбце семь троек (7 · 3), но в первом — три семерки (3 · 7).и т. д.
Отсюда следует, что результаты сложения чисел в обоих столбцах должны быть одинаковыми. Убедитесь в этом.
Ответ 43.
В первой и пятой строках числа единиц дополняют друг друга до 10, а числа десятков, сотен и всех остальных разрядов соответственно дополняют друг друга до 9, следовательно, сумма чисел в этих двух строках равна 1 000 000.
Та же особенность обнаруживается и в остальных трех парах чисел: втором и шестом, третьем и седьмом, четвертом и восьмом.
Сумма каждой пары чисел равна 1 000 000. Значит, сумма всех восьми чисел равна 4 000 000.
Ответ ко второму фокусу. Вероятно, вы догадались, что приписывается такое число, все цифры которого дополняют до числа 9 цифры одного из двух написанных чисел, например второго. При этом условии последняя цифра суммы, очевидно, будет на 1 меньше последней цифры первого слагаемого, а все остальные цифры суммы будут такие же и в том же порядке, как и у первого слагаемого, а самой первой цифрой суммы будет всегда 1.
Таким образом, начиная писать сумму слева направо, напишите 1, затем повторите все цифры первого слагаемого, кроме последней, которую надо уменьшить на 1.
Попрактикуйтесь, прежде чем будете показывать товарищам математические фокусы.
Ответ 44.
Пусть монета с четным числом копеек (например, двухкопеечная) — в правой руке, а монета с нечетным числом копеек (например, трехкопеечная) — в левой. Тогда утроенное четное число останется числом четным и удвоенное нечетное будет тоже четным, а сумма четных чисел тоже обязательно четная.
Пусть теперь монета с нечетным числом копеек (например, трехкопеечная) — в правой руке, а монета с четным числом копеек (например, двухкопеечная) — в левой. Тогда утроенное нечетное число останется числом нечетным, а удвоенное четное будет числом четным. Сумма же чисел нечетного и четного обязательно нечетная.
Разнообразить фокус можно так: предлагать умножать содержимое правой руки не обязательно на 3, а вообще на любое нечетное число, а содержимое левой руки — на любое четное число.
Ответ 45.
4 брата и 3 сестры.
Ответ 46.
22+2+2+2 и 888+88+848+8.
Ответ 47.
100=111—11, 100=5 · 5 · 5 — 5 · 5, 100=5 · 5 · (5 — 5/5), 100=(5+5+5+5) · 5,
Ответ 48.
Если действовать планомерно, то можно найти все варианты решения (см. схему на следующей странице). Сначала рассматриваем возможные замены нулями цифр последнего столбца (сумма цифр должна иметь последней цифрой единицу). Это дает три варианта (на схеме обозначены буквами А, Б, В). Зная сумму цифр, оставленных в последнем столбце, подбираем цифры для среднего столбца (на схеме случаи А-1. 2, 3, Б-1, 2, 3, 4, В-1, 2, 3) и аналогично для первого столбца (нижний ряд на схеме).
Схема показывает, что имеется 18 вариантов решения задачи, из них в одном случае можно заменить нулями 5 цифр, в одном
случае—б цифр, в трех случаях—7 цифр, в шести случаях—8 цифр, в пяти случаях — 9 цифр и в двух случаях — 10 цифр.
Невозможно сохранить сумму 1111, заменяя нулями более десяти и менее пяти цифр.
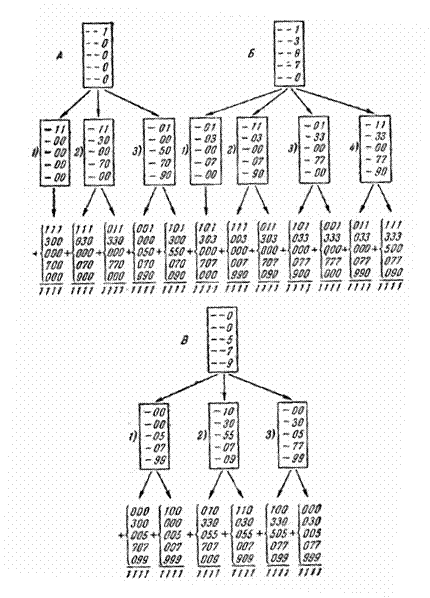
К задаче 48.
Ответ 49.
Подобно тому как заполнение ящика предметами разной величины начинают с наибольших предметов, так и составление заданной суммы лучше начинать с наибольших возможных слагаемых. По условию, слагаемыми должны быть восемь нечетных чисел.
Рассуждаем так.
Ни одно из чисел 19, 17 и 15 не может быть слагаемым, так как в каждом из этих случаев не наберется остальных семи слагаемых. Если взять слагаемым число 13, то для составления числа 20 необходимо и достаточно прибавить к 13 семь раз по 1:
13+1+1+1+1+1+1+1= 20.
Если первое слагаемое 11, то вторым слагаемым не могут быть 9, 7 или 5 (не набирается необходимого числа остальных слагаемых). Пробуем 3:
11+3=14.
До 20 остается 6 единиц и нам нужно б слагаемых. Следовательно, получаем второе решение:
11+3+1+1+1+1+1+1=20.
Берем первым слагаемым число 9. Число 7 не может быть вторым слагаемым (9+7= 16; остается 4 единицы на 6 слагаемых). Попробуем 5. Имеем:
9+5=14.
На 6 слагаемых остается 6 единиц. Это возможно. Получаем третье решение:
9+5+1+1+1+1+1+1=20.
Пробуем 3. Имеем:
9+3=12.
Остается 8 единиц на 6 слагаемых. Прибавим еще 3. Тогда
9+3+3= 15.
Остается 5 единиц на 5 слагаемых. Получаем четвертое решение:
9+3+3+1+1+1+1+1=20.
Система проб, я думаю, теперь ясна. Продолжайте рассуждения самостоятельно, полагая первым слагаемым 7, а затем 5 и 3. Всего получится 11 следующих решений:
13+1+1+1+1+1+1+1=20,
11+3+1+1+1+1+1+1=20,
9+5+1+1+1+1+1+1=20,
9+3+3+1+1+1+1+1=20,
7+7+1+1+1+1+1+1=20,
7+5+3+1+1+1+1+1=20,
7+3+3+3+1+1+1+1=20,
5+5+5+1+1+1+1+1=20,
5+5+3+3+1+1+1+1=20,
5+3+3+3+3+1+1+1=20,
3+3+3+3+3+3+1+1=20,
Есть только одно решение (шестое сверху), которое приводит к сумме, состоящей из наибольшего числа (из четырех) неодинаковых слагаемых.
Ответ 50.
Непосредственно считать все возможные маршруты от А до С сложно — запутаетесь. Надо начать с подсчета маршрутов до перекрестков, более близких к начальному пункту А (см. рисунок).
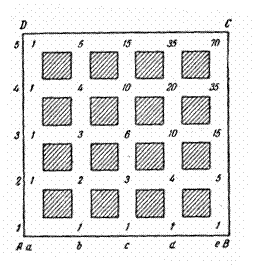
К задаче 50.
Очевидно, что в каждый перекресток, находящийся на сторонах АВ
и AD, ведет только один путь; в перекресток 2b ведут 2 пути, В перекресток 2с можно попасть, во-первых, из пункта 2b, значит, тоже двумя маршрутами, и, во-вторых, из пункта 1с, то есть еще одним маршрутом. Следовательно, всего к перекрестку 2с ведут 2+1=3 маршрута (найдите их). Аналогично рассуждая, получим, что и к перекрестку 3b ведут 3 маршрута.
В перекресток Зе ведут те же 3 маршрута, которыми можно попасть в перекресток 3b, и те 3 маршрута, которыми можно попасть в перекресток 2с, то есть всего 6 маршрутов. Продолжая эти рассуждения, заметим, что вообще количество маршрутов, ведущих к любому перекрестку, равно сумме маршрутов, ведущих к двум смежным перекресткам, расположенным слева и снизу от рассматриваемого. Если, например, мы определили, что число маршрутов, ведущих в Зс, равно 6, а в 2d
равно 4, то число маршрутов, ведущих в 3d, будет равно 10 и т. д.
Так можно определить число маршрутов, ведущих из начального пункта А к любому перекрестку. К конечному пункту С, таким образом, можно прийти 70 различными путями.
(Число маршрутов равно С48; вообще Сnm+n , где m число кварталов вдоль АВ, n – число кварталов вдоль ВС.)
Ответ 51.
Если на концах какого-либо диаметра поместить числа A и a, а на концах соседнего диаметра поместить числа В и Ь, то, по условию, А+В=а+Ь, Отсюда А—а=Ь—В, то есть разности противоположно расположенных чисел должны быть равны между собой.
В этом ключ к отысканию всех решений задачи.
Очевидно теперь, что для решения задачи надо разбить все данные целые числа от 1 до 10 на 5пар с одинаковыми разностями чисел в каждой паре. Простое испытание показывает, что возможны только 2 группы пар, удовлетворяющих этому условию:
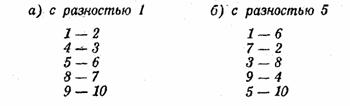
Расположив эти числа по кругу, получаем два основных решения (см. рисунок). Все остальные решения можно образовать из основных, перемещая пары чисел с одного диаметра на другой, так как чередование пар внутри одной группы может быть произвольным.
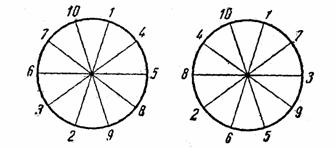
К задаче 51.
Так, рядом с парой 1—2, разместившейся на первом диаметре, можно поместить на втором диаметре пару 4—3, или пары 6—5,8—7, или 10—9.
Это дает четыре различных решения. В каждом из получающихся положений на третьем диаметре можно поместить любую из оставшихся трех пар. Это дает 4X3=12 решений. В каждом из них две возможности для размещения оставшихся двух пар на четвертом и пятом диаметрах. Это приводит к 12X2=24 решениям для каждой группы пар чисел.
Всех решений 48. (Число решений равно удвоенному числу перестановок из четырех элементов: 2 · P4.)
Ответ 52.
Из четырех чисел возможна только одна группа:
1+1+2+4=1x1x2x4.
Из пяти чисел — три:
1+1+1+2+5=1х1×1х2×5,
1+1+1+3+3=1х1×1х3×3,
1+1+2+2+2=1×1х2х2×2.
Требуемые группы из 6 или 7 и т.д. чисел по аналогии составьте самостоятельно. Возьмите, скажем, два числа 2 и 6 и их сумму 2+6 дополняйте единицами до произведения 2х6—12, а произведение 2х6 в свою очередь умножайте на соответствующее количество единиц.
Ответ 53.
9+8+7+65+4+3+2+1=99 или 9+8+7+6+5+43+21 = 99; 1 + 2+34+ +56+7=100 или 1+23+4+5+67=100.
Ответ 54.
Возможное решение показано на рисунке.

К задаче 54.
Ответ 55.
Одно из возможных решений представлено на рисунке. Путь одного геолога изображен сплошной линией, а путь другого— пунктиром. Оба геолога обошли ровно по 40 клеток поля, побывав на каждой клетке по разу.
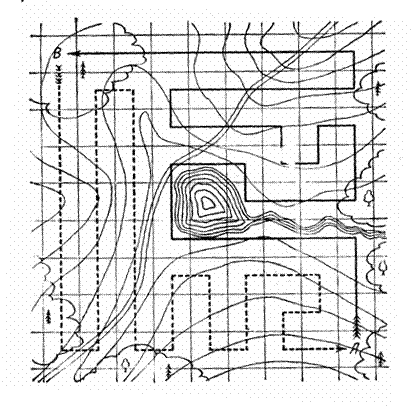
К задаче 55.
Ответ 56.
Любая, придуманная вами и ведущая к цели последовательность перемещений спичек будет лишь вариантом основное схемы решения, по которой обязательно должны быть созданы пара спичек на краю данного ряда и по одной паре на вторых
спичках от краев ряда, образовавшегося из восьми спичек после выделения крайней пары.
Ответ 57.
Чтобы легко было пользоваться указанной далее схемой перемещения спичек, напишите на бумаге 15 целых чисел, начини с 1, и над каждым числом расположите спички, так:
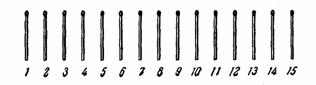
Перемещайте спички в таком порядке: 5 к 1, 6 к 1 или схематично: 5→1, 6→1,9→3, 10→3,8→14,7→14, 4→2,11→2, 13→15, 12→15,
Заметьте, что решение строится по той же схеме, что и в предыдущей задаче: создается тройка спичек на краю данного ряда и по одной тройке на вторых спичках от краев ряда, образовавшегося из двенадцати спичек, остающихся после выделения крайней тройки.
Всякий иной порядок перемещения спичек дает лишь вариант приведенного решения.
Рассуждения, приведенные в тексте задач 56 и 57, показывают, что для превращения пар спичек в ряд требуется самое меньшее 4 пары (8 спичек), для превращения троек спичек в ряд требуется самое меньшее 4 тройки (12 спичек). Эти же рассуждения остаются в силе и для групп, содержащих по 4, по 5, …, по n
спичек: каждый раз необходимо иметь самое меньшее 4 группы (4 n спичек). Отсюда следует, что для составления групп по n спичек в каждой достаточно иметь 4 n спичек, расположенных в ряд, но можно иметь и 5 n, 6 n, 7 n и т. д. спичек. То есть в группы по n
спичек можно расположить kn спичек, где k≥4.
Ответ 58.
Вся «изюминка» решения заключается в том, что, уходя из дома, я догадался пустить в ход свои стенные часы и заметить по ним, в котором часу я вышел, а затем — в котором часу вернулся. Так, по своим часам я смог определить, сколько времени я отсутствовал. Придя к знакомому и уходя от него, я заметил показания его часов. Это дало мне возможность определить продолжительность пребывания у знакомого.
Вычитая из продолжительности времени, которое я отсутствовал дома, продолжительность пребывания у знакомого, я получил количество времени, затраченного на дорогу туда и обратно. Прибавив половину этого количества времени к показанию часов товарища, когда я от него уходил, я в сумме получил то показание часов, на которое следовало поставить мои стенные часы.
Ответ 59.
Первое решение. Не придется много размышлять для составления первых двух равенств:
(1+2):3 = 1, 12:3:4 = 1.
Для составления третьего равенства повторяем действие первой строки, прибавляем предпоследнее число (4) и результат делим на последнее число (на 5):
((1 + 2):3+4):5 = 1.
Этот прием составления равенств можно повторить последовательно для всех строк с нечетными номерами, то есть, например, для составления пятого равенства повторяем действия третьей строки, прибавляем предпоследнее число (6) и результат делим на последнее число (на 7) и т. д.
Аналогичным путем на основе второго равенства составляем требуемые равенства последовательно и для всех строк с четными номерами. Окончательно,
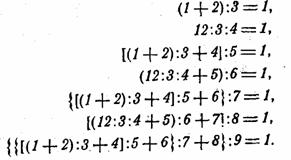
Действия вычитания, как видите, нет. Второе решение.
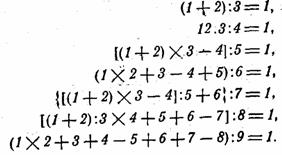
В этом решении использованы знаки всех четырех действий арифметики.
Ответ 60.
Счетчик машины показывал 15 951. Цифра десятков тысяч не могла измениться через 2 часа. Следовательно, первой и последней цифрой нового симметричного числа остается 1. Цифра тысяч могла и должна измениться, так как за 2 часа машина прошла, конечно, больше 49 км, но никак не больше 1000 км; следовательно, цифра тысяч, а вместе с нею и цифра десятков — 6.
Очевидно, что цифра сотен — 0 или 1, и счетчик показывал либо число 16 061, либо число 16 161.
Число сотен вряд ли могло достигнуть 2, так как в этом случае получилось бы, что машина за 2 часа прошла
16 261 — 15 951=310 км, а такая скорость пока не характерна для машин неспортивного типа,
Если счетчик показал число 16 061, то машина прошла за 2 часа 16 061—15 951— 110 км и, следовательно, имела скорость 110 : 2=55 км в час.
Во втором случае скорость — 105 км в час.
Ответ 61.
Для решения задачи надо знать количество приборов, смонтированных бригадиром. А для этого в свою очередь надо знать, сколько приборов в среднем было смонтировано каждым из 10 членов бригады. Распределив поровну между девятью юными рабочими 9 приборов, изготовленных добавочно бригадиром, мы узнаем, что в среднем каждый член бригады смонтировал 15+1= 16 приборов.
Отсюда следует, что бригадир изготовил 16+9=25 приборов, а вся
бригада (15×9)+25=160 приборов.
Знающие алгебру могут решить эту задачу путем составления одного уравнения с одним неизвестным.
