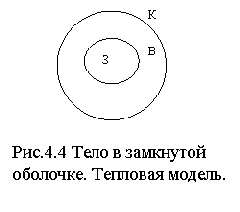
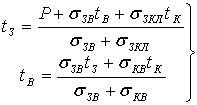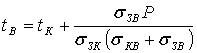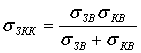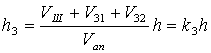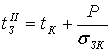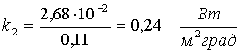Рассмотрим систему тел (рис.4.4), состоящую из оболочки К газообразной среды В, заполняющей её свободный объём, и тела З, расположенного внутри оболочки. Пусть в теле действует источник тепла Р. Между телом и газом, а также между газом и оболочкой происходит конвективный теплообмен, тело и оболочка обмениваются тепловой энергией путём кондукции и излучения.

Температура t_k оболочки, геометрические и физические параметры тел и среды заданы.

Для расчёта средней поверхностной температуры t_S тела и средней объёмной температуры среды t_B, заполняющей оболочку, применим формулу:

(4.24)

где s_зв, s_кв – конвективная теплопроводность между телом, средой и оболочкой; s_зкл – лучистая проводимость между телом и оболочкой. Решая систему (4.24) относительно t_з и t_в получим:

(4.25)

(4.26)

(4.27)

(4.28)

Рассмотрим тепловой режим ЭВА, нагретая зона которого состоит из крупных элементов. Пусть ЭВА имеет герметический корпус в форме прямоугольного параллелепипеда (рис.4.5).

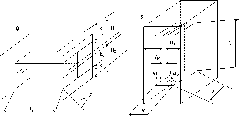Рис.4.5 Эквивалентные нагретые зоны в аппарате при вертикально и

горизонтально ориентированном шасси (Н₁ и Н₂ – расстояние от шасси

до параллельных ему стенок корпуса; d₁ и d₂ – толщина зазоров между

нагретой зоной и стенками корпуса; l₁, l₂, h_З – размеры зоны).

Будем считать, что ЭВА есть простейшая система тел, состоящая из оболочки (корпуса), тела (эквивалентной нагретой зоны с источником тепла) и среды (воздуха, заполняющего свободный объём корпуса). Средняя поверхностная температура t_З нагретой зоны вычисляется, если известна s_ЗК. Если нет, то для определения s_ЗК нужно знать размеры эквивалентной нагретой зоны и толщины зазоров, отделяющих её от корпуса. Будем считать, что размеры основания параллелепипеда l₁ и l₂ равны соответствующим размерам шасси, а высоту h_З определим из условия равенства объёмов реальной и эквивалентной нагретой зон. При этом:

h_З = h_З1 + h_З2 + d_Ш (4.29)

,

где V₃₁ и V₃₂ – суммарные объёмы элементов, распределённых по обе стороны шасси; V_Ш и d_Ш – объём и толщина шасси. Выразим h₃ через h корпуса и его коэффициент заполнения.

(4.30)

Толщина зазоров d₁ и d₂ вычисляются по формулам:

d₁ = Н₁ – h₃₁ и d₂ = H₂ – h₃₂ , (4.31)

а V_ап = l₁ l₂ h , Н₁ и Н₂ – известны из чертежей.

Лучистую проводимость получают из формулы s_ЗКЛ = a_ЗЛ + S_ЗЛ , где a_ЗЛ=e_прзкj_зкf(t_з, t_к) – коэффициент теплообмена излучением между корпусом и нагретой зоной; S_ЗЛ = 2l₁ l₂ + 2h_з (l₁ + l₂) – площадь излучающей поверхности нагретой зоны. Обычно j_зк=1 так как практически вся энергия достигает корпуса.

При расчёте конвективного переноса тепла от нагретой зоны учтём, что условия теплообмена отдельных поверхностей параллелепипеда и корпуса неодинаковы вследствие их различной ориентации и разных расстояний друг от друга.

, (4.32)

где k_i – коэффициент конвективно-кондуктивной теплопередачи через i-й зазор. Для зазора вверх случай а) (рис.4.5) и обоих зазоров случай б) имеем

.

Для зазора вниз случая а) (рис.4.3.2) имеем

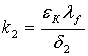— для плоской поверхности, где l_f –коэффициент теплопроводности среды в прослойке. При всех вычислениях , тогда

(4.33)

Площадь зоны для конвекции: S₃₁ = S₃₂ = l₁ l₂ ; S₃₃ = 2h₃(l₁ l₂).

Далее получим s_ЗК = s_ЗКЛ + s_ЗКК.

Для получения конкретных цифр используем метод последовательных приближений, задавая температуру нагретой зоны примерно равной

. (4.34)

Затем определим все параметры и получаем

. (4.35)

Если t_З^II » t_З^I , то расчёт окончен, если нет – всё повторяется с исходных позиций.

Для расчёта температуры воздуха предложена формула

, (4.36)

откуда получаем

. (4.37)

Подставляя (4.37) в (4.36) после простых преобразований получаем

(4.38)

Пример:

Вычислить температуру нагретой зоны электронного аппарата с горизонтальным шасси, если L₁=0,585 м; L₂=0,380 м; h=0,384 м; Р=103 Вт; t_к=30°С; k_зап=0,29; d₁=0,16 м; h_з=0,11 м; d₂=0,11 м; толщина корпуса d_к=0,002 м; e=0,9 для всех внутренних поверхностей.

Пусть t_З^I=20 + 3(30 — 20) = 50°С

Тогда e_прзк=e_з e_к= 0,81; a_зл=0,81?f(50;30)=0,81?6,98=5,65 Вт/м²град

l₁= L₁ — 2d_к = 0,585 — 0,004 = 0,581 м; l₂= L₂ — 2d_к = 0,376 м

S_зл=2?0,581?0,376+2?0,11(0,581+0,376)=0,646 м²

s_зл=5,65?0,646=3,65 Вт/град

Далее: t_m=1/2(t_з + t_к)=40°С; l=2,68?10^-7 Вт/м?град (справочник)

А₅(t_m)=0,59 Вт/м^1,75град^1,25

s_зкк1=7,70?0,376?0,581=1,71 Вт/град

s_зкк2=0,24?0,376?0,581=0,05 Вт/град

s_зкк3=4,02?2?0,11?(0,376+0,581)=0,84 Вт/град

Вт/град

s_зк = s_зкл + s_зкк =3,65 + 2,60 = 6,25 Вт/град

Далее .