Лабораторная работа №5.

1. Что называется симплексом?

Симплекс – простейшая выпуклая геометрическая фигура. Под n-мерным симплексом в n-мерном пр-ве понимают фигуру, образованную мн-вом (n+1) вершин, не принадлежащих одновременно ни одному (n-1) мерному пр-ву данного n-мерного пр-ва. Число вершин симплекса на 1 больше размерности пр-ва. В двумерном пространстве симплексом является любой треугольник, а в трехмерном пространстве – любая треугольная пирамида.

Симплекс называется регулярным, если расстояние между вершинами одинаково.

4. Каковы критерии достижения оптимума?

Оптимум считается достигнутым, если

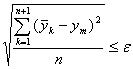(абсолютные единицы), или, если одна и та же вершина входит в последовательные симплексы N раз, где

5. Каковы преимущества и недостатки симплексной оптимизации?

Преимущества и недостатки метода:

1. Каждый дополнительный фактор требует постановки только одного опыта.

2. Метод чрезвычайно прост с точки зрения объема вычислений.

3. Ограничения на область изменения факторов учитываются при движении симплекса.

4. Чем больше число факторов, тем больше эффективность метода.

5. Направление движения определяется соотношением только величины целевой функции в вершине симплекса, а не их абсолютным значением.

6. Направление движения может лишь в незначительной степени отличаться от крутого восхождения.

7. Метод может быть использован в случае дрейфа характеристик объекта.

Недостатки.

1. Реализация метода не даёт информации о влиянии каждого фактора на целевую функцию.

2. Движение по правилам симплексного метода даёт ограниченное представление о характере поверхности объекта.

6. От чего зависит эффективность метода?

Чем больше число факторов, тем больше эффективность метода.

7. Можно ли использовать симплексный метод в случае дрейфа характеристик объекта?

Метод может быть использован в случае дрейфа характеристик объекта, что является преимуществом данного метода.

8. Можно ли с помощью симплекс метода определить степень влияния факторов на целевую функцию?

Реализация метода не даёт информации о влиянии каждого фактора на целевую функцию.

2. Какие существуют методы задания координат начального симплекса?

1. Способ

Базовая точка (в нее помещается начало координат) – (0, 0, …, 0). Из базовой точки (1) проводим 2 луча под углом a к осям X₁ и X₂. Строим равносторонний треугольник (1)(2)(3).

Оси нашего пр-ва различные. Пусть длина ребра будет равна l, тогда получим следующие соотношения: ; .

№ вер-ны	x1	x2	x3	…	xn-1	xn
1	0	0	0	…	0	0
2	P	q	q	…	q	q
3	Q	p	q	…	q	q
…	…	…	…	…	…	…
n	Q	q	q	…	p	q
n+1	Q	q	q	…	q	p

Теперь запишем координаты вершин в тех системах координат, в которых будем проводить эксперимент.

№ вершины	Координаты
X1	x2	x3	x4	…	xn-1	xn
1	X*1	X*2	X*3	X*4	…	X*n-1	X*n
2	X*1+p? X1	X*2+q? X2	X*3+q? X3	X*4+q? X4	…	X*n-1+q? Xn-1	X*n+q? Xn
3	X*1+q? X1	X*2+p? X2	X*3+q? X3	X*4+q? X4	…	X*n-1+q? Xn-1	X*n+q? Xn
4	X*1+q? X1	X*2+q? X2	X*3+p? X3	X*4+q? X4	…	X*n-1+q? Xn-1	X*n+q? Xn
…	X*1+q? X1	X*2+q? X2	X*3+q? X3	X*4+p? X4	…	X*n-1+q? Xn-1	X*n+q? Xn
N	X*1+q? X1	X*2+q? X2	X*3+q? X3	X*4+q? X4	…	X*n-1+p? Xn-1	X*n+q? Xn
N+1	X*1+q? X1	X*2+q? X2	X*3+q? X3	X*4+q? X4	…	X*n-1+q? Xn-1	X*n+p? Xn

В данном способе задания симплекса точки остаются неподвижными + минимум вычислений.

2.Способ

Центр симплекса помещается в центр координат.

№ вер-ны	x1	X2	x3	…	xn-1	xn
1	-r1	-r2	-r3	…	-rn-1	-rn
2	R1	-r2	-r3	…	-rn-1	-rn
3	0	R2	-r3	…	-rn-1	-rn
…	…	…	…	…	…	…
n	0	0	0	…	Rn-1	-rn
n+1	0	0	0	…	0	Rn

, . Если величины p и q зависели от n, то r_i и R_i не зависят от n. Так же позволяет варьировать центром тяжести фигуры.

Таблица координат в натуральной с-ме единиц.

№ вершины	Координаты
x1	x2	X3	X4	…	xn-1	Xn
1	X*1-r1DX1	X*2-r2DX2	X*3-r3DX3	X*4-r4DX4	…	X*n-1-rn-1DXn-1	X*n-rnDXn
2	X*1+R1DX1	X*2-r2DX2	X*3-r3DX3	X*4-r4DX4	…	X*n-1-rn-1DXn-1	X*n-rnDXn
3	X*1	X*2+R2DX2	X*3-r3DX3	X*4-r4DX4	…	X*n-1-rn-1DXn-1	X*n-rnDXn
4	X*1	X*2	X*3+R3DX3	X*4-r4DX4	…	X*n-1-rn-1DXn-1	X*n-rnDXn
…	…	…	…	…	…	…	…
N	X*1	X*2	X*3	X*4	…	X*n-1-+Rn-1DXn-1	X*n-rnDXn
N+1	X*1	X*2	X*3	X*4	…	X*n-1	X*n+RnDXn

3. Какова процедура поиска оптимума целевой функции симплексным методом?

Алгоритм процедуры

0. Сделаем начальный симплекс.

1. Подбираем величину шага DX₁, так, чтобы изменение каждого фактора на целостную единицу (шаг) приводило приблизительно к одинаковым изменениям целевой функции.

2. Рассчитываем координаты начального симплекса и однократно реализуем соответствующие опыты.

3. Отбрасываем точку плана с наименьшим значением целевой функции и строим новый симплекс. Новый симплекс образуется оставшимися вершинами исходного симплекса и новой вершиной, получаемой путем зеркального отображения отброшенной вершины, относительно противоположной ей (n-1)ой грани исходного симплекса. Координаты новой точки вычисляются по формуле: , j – номер вершины исходного симплекса с наименьшим значением целевой функции.

В данной точке снова проводится эксперимент ? получаем новый симплекс. Для контроля правильности проведенного опыта в новой вершине можно подсчитать теоретическое: , если экспериментальному значению в jой точке ? все нормально.

4. В новом симплексе снова находим вершину с наименьшим значением и отбрасываем ее. Пересчитываем ее по вышеизложенному алгоритму (методу). Т. о. происходит последовательное перемещение симплекса в процессе, которого на каждом шаге отбрасывается вершина симплекса с наихудшим значением целевой функции. При этом направление движения центра симплекса колеблется около направления градиента.

5. Если при перемещении симплекса на протяжении (n+1) шагов та или иная сохраняет свое положение, то симплекс совершает оборот вокруг этой вершины. В данной точке или ее окрестности находится оптимум целевой функции, либо значение целевой ф-ии в этой вершине определено неверно. Для уточнения ситуации вновь проводится эксперимент, и в дальнейшем принимают во внимание только новое значение целевой функции.

6. Если по ходу движения окажется, что целевая функция в новой вершине вновь образованного симплекса оказывается меньше, чем в остальных, то в соответствии с логикой движения следует возвратиться к предыдущему симплексу и в качестве отбрасываемой вершины выбрать ту вершину, в которой значение целевой функции имеет значение следующее по порядку за наихудшей вершиной симплекса. Так же поступают, если новая вершина выходит за рамки допустимой области планирования.

7. При достижении области оптимума, для уточнения (локализации) точки оптимума размер симплекса следует уменьшить (как правило на ? начальной величины).

8. Если ошибка эксперимента относительно велика, целесообразно в каждой точке симплекса ставить несколько опытов и использовать усредненные значения целевой функции.

9. Оптимум считается достигнутым, если

(абсолютные единицы)