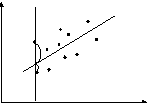
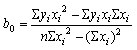Пусть есть n пар экспериментальных данных состоящих из значений управляемых элементов X и значений функции отклика.

Необходимо провести некоторую линию через эти точки, вокруг которой группировались бы эти данные. В случае применения метода наименьших квадратов кривая проводится т.о. чтобы сумма квадратов отклонения от точек на данной кривой до экспериментальных точек была минимальной.

Предположим вид связи: или . Пусть у нас постулирована линейная связь.

. Решение сводится к решению системы уравнений.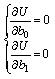

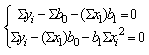
Свойства оценок полученных методом наименьших квадратов

1. Эти оценки являются несмещенными, т.е. мат. Ожидание этих оценок равно истинному значению оцениваемого параметра.

2. Она (оценка) является состоятельной, т.е. она сходится по вертикали к истинному значению при неограниченном увеличении числа пар наблюдений n.

3. Она является эффективной, т.е. обладает наименьшей дисперсией среди всех остальных линейных оценок.

Подобные вычисления производятся в таблице.X Y X² Y² XY X+Y (X+Y)²

Внизу таблицы подбивается сумма.