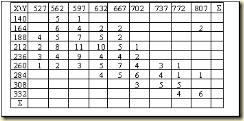
Пусть есть двумерная СВ x, y. Разобьем область определения каждой СВ на k интервалов (как при построении гистограммы) и представим это в виде некоторой таблицы.

Если в таблице двумерного распределения есть одиноко стоящая заполненная клетка, вокруг которой есть хотя бы по одной пустой клетке – то это двумерное выделяющееся значение. Таблица двум-го распр-я позволяет выделить: а) двумерные выделяющиеся значения; б) определить знак связи; в) пределить вид связи. Для построения ур-я связи используется метод: а) наименьших квадратов; б) Чебышева; в) наименьших модулей; г) наименьших квадратов с предварительной ортогонализацией факторов; д) главных компонент; и т.д. Регрессионная модель, получаемая с помощью метода наименьших модулей – это зависимость медианы выходной величины от значений управляемой величины, а остальные позволяют получить регрессионную модель, описывающую зависимость среднего арифметического выходной величины от значений управляемой величины. Т.о. статистическая сущность регрессионных моделей полученных с помощью метода наименьших модулей и с помощью остальных методов различна. В дальнейшем будем рассматривать регрессионные модели относительно среднего арифметического.

. Корреляционное соотношение характеризует тесноту связи как линейной, так и нелинейной. . Корреляционное отношение менее удобно для характеристики тесноты связи.