Метод Тьюки позволяет проверить гипотезу о равенстве средних арифметических нескольких выборок одинакового объекта. Т.к. выборки взяты из нормальных совокупностей, то сущуствует некоторый интервал TS, внутри которого центры выборок статистически неразличимы. , где — стьюдентизированный размах..

 

— средняя выборочная дисперсия с числом степеней свободы. Интервал статистической неразличимости..

Гипотезы о равенстве выборочных дисперсий.

Пусть есть две выборки объёмами n1 и n2. Требуется проверить гипотезу о равенстве их выборочных дисперсий. и

Критерий Фишера.

Необходимо найти следующую величину:
(в числитель ставят наибольшую дисперсию).

Если:, то гипотезу о равенстве дисперсий принимают.

Критерий Кохрена.

Критерий Кохрена позволяет проверить гипотезу о равенстве выборочных дисперсий нескольких выборок одинакового объема.и .

Для этого находят следующую величину: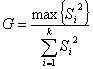. Если : , то принимают основную гипотезу.

Критерий Бартлетта.

Критерий Бартлетта позволяет проверить гипотезу о равенстве выборочных дисперсий нескольких выборок различного объема. Для этого находят следующую величину: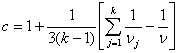, где и
Средневзвешенная дисперсия:, Если: , то гипотезу принимают.