1. По MAX относительного отклонения (ищем элемент с максимальным отклонением) – метод Ирвина.

2. По MIN относительного отклонения (ищем элемент с минимальным отклонением).

Исходные данные:

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
182	172	180	182	180	178	178	180	178	180	175	160	174	189	184	164	178	173	178

1. (среднее арифметическое) = 177.10 ; (эмпирическая дисперсия) =6.65

Для малых выборок =

2. Находим величину == 1.78, сравниваем найденное значение с _{табличн.}(5%,N) = 2.5 (Квантили распределения).

3. Т.к. полученное < _{табличн.} , то следовательно значение принадлежит данной выборке.

4. Ищем элемент с MIN относительного отклонения, – находится под номером 12 – 160.

5. Исключаем его и пересчитываем величины (среднее арифметическое) = 178.05 ; (эмпирическая дисперсия) =5.35

6. Находим величину = = =3,36, сравниваем найденное значение с _{табличн.}(5%,N-2) = 2.11 (t -распределение Стьюдента) (Если объем выборки 80 –150 , то = )

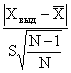7. Так как величина > _{табличн.}, то, следовательно, мы отбрасываем данное значение из исследуемой выборки.