Корреляция выражает такую форму связи, когда определенному значению одной величины соответствует ряд распределения значений другой величины. Так как при корреляционной зависимости каждому X соответствует целый ряд значений Y, то они образуют в системе координат некое «корреляционное поле» величины. Например, более высокой квалификации работников соответствует более высокая зарплата, хотя среди них могут быть люди с разной зарплатой.

Корреляционно связаны условия труда и удовлетворенность работой, образование родителей и успеваемость детей, стаж работы и производительность труда. Наличие корреляции свидетельствует о том, что, либо одно из выделенных явлений частичная причина другого, либо оба явления — следствие общих причин. Но выявление корреляции не дает оснований утверждать о причинно — следственной связи явлений. Так, В. Шубкин обнаружил корреляцию между зарплатой родителей и успеваемостью их детей — школьников; Ричардсон между зарплатой учителей и потреблением вин в США.

В первом случае корреляция объясняется тем, что, как правило, более образованные родители получали более высокую зарплату, а во втором — тем, что в этот период (1870-1910гг.) в США росла зарплата (в т. ч. и учителей) и соответственно увеличивалось потребление продуктов (в т. ч. и вина), т. е. и зарплата учителей и потребление вина были следствием общих причин, а не причиной и следствием по отношению друг другу.

Показатели, отражающие меру корреляции (тесноту, направление связи) называются коэффициентами корреляции. В социологии применяются коэффициент Юла (Q), коэффициент двусторонней связи (Ф), Пирсона (R), ранговой корреляции Спирмена ( ), множественный коэффициент корреляции (W), коэффициент Чупрова (Т) и Крамера (К).

Чтобы найти связи между двумя признаками, необходимо составить двухмерную таблицу. Например, нужно установить связь между удовлетворенностью работников профессией Y (Y1 — удовлетворен, Y2 — не удовлетворен) и производительностью труда X (X1 — высокая, X2 — низкая). Пусть из N=100 чел. 50 удовлетворены (Y1=50), а 50 не удовлетворены (Y2=50). Y 20 человек высокая (X1=20), а у 80 низкая (X2=80) производительность труда.

Обнаружена прямая (функциональная) односторонняя связь между производительностью труда и удовлетворенностью профессией.

Для случая

Теперь связи между производительностью труда и удовлетворенностью профессий нет: и у работников с высокой и у работников с низкой производительностью одинаковы числа удовлетворенных и неудовлетворенных профессией.

Q — показатель односторонней связи. Например, если B=0, то Q=1. Это значит, что в исследуемой группе высокая производительность сочетается с удовлетворенностью, но это не означает, что все удовлетворенные профессией характеризуются высокой производительностью.

Построим т. н. корреляционную двумерную таблицу:

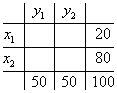
Заполненные внешние клетки называются маргинальными. Но пока мы не знаем распределение респондентов по внутренним клеткам, мы ничего не можем сказать о связи между признаками X и Y. Для удобства обозначим внутриклеточные частоты буквами.

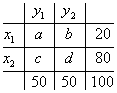
Рассмотрим коэффициент Юла . Пусть внутриклеточные частоты такие . Это значит, что все 20 респондентов с высокой производительностью труда (X1) удовлетворены своей профессией (Y1), но не наоборот (среди людей, удовлетворенных профессией (50 чел.) и 30 человек имеют низкую производительность труда).

Q=1 означает обратную связь — высокая производительность соответствует низкой удовлетворенности (в указанном случае). Для описания двусторонней связи используется коэффициент

Если обращается в 1, когда хотя бы одна из внутриклеточных частот равна 0, то =1, если либо A=С=0, либо B=D=0.

Наиболее широко известной мерой корреляции является коэффициент Пирсона (R).

Для расчетов используется двухмерная корреляционная таблица вида (в качестве примера ниже приводится таблица соотношения двух признаков (X) общий стаж работы и зарплата (Y) в группе респондентов 25 человек).

№ респондента	Стаж лет	Зарплата рублей
1 2 3 …	20 21 2 …	190 180 130 …	400 441 4 …	36100 32400 16900 …	3800 3780 260 …
N=25

Коэффициент Пирсона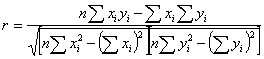

Подставляем данные из таблицы:

Для проверки статистической значимости полученного коэффициента (не обусловлена ли полученная величина R =0,86 случайностью) при N< 50 применяется критерий T, вычисляемый по формуле ; .

Для случая N>50 используется критерий . Если полученная (эмпирическая) величина T(Z) больше табличной (критической, ожидаемой), то полученный коэффициент (в нашем примере 0,86 значим с заданной вероятностью . если = 0,01, значит лишь в одном из 100 случаев R=1).

Коэффициенты ранговой корреляции Спирмена ( ), Кендала ( ) измеряют взаимосвязь между упорядоченными рядами признаков по степени нарастания или убывания.

Коэффициент Спирмена 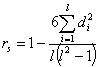, где

– разность между I-ми парами рангов;

L – число пар рангов

Величина =1, если оба ряда ранжируются в одном (однонаправленном) порядке (убывания или нарастания). = -1 при обратной направленности проранжированных рядов. =0 означает полное взаимное беспорядочное расположение рангов. Для расчетов используется корреляционная таблица вида (в качестве примера приводится таблица о жизненных планах рабочей и крестьянской молодежи).

Жизненные планы	Социальное происхождение (в %)	Ранг I	Ранг II
Из рабочих	Из крестьян
Получить высшее образование	57,5	51	1	3,5	-2,5	6,25
Получить интересную работу	57,3	59	2	1	1	1
Побывать в других странах	53,8	52	3	2	1	1
Создать хорошие жилищные условия	49,7	51	4	3,5	0,5	0,25
Материальное благополучие	48,5	50	5	5	5	0

Значимость коэффициента корреляции для определяется по таблице критических величин . Для критические значения находятся на необходимом уровне значимости по таблице и сравниваются с наблюдаемыми по формуле

Если Z критическое превышает ZТабл, то можно сделать вывод, что есть значимая связь между ранжированными признаками. В нашем примере между предпочтениями жизненных планов рабочей и крестьянской молодежи.

Для анализа многомерных взаимосвязей и взаимозависимостей используются различные средства анализа. Одним из распространенных многомерных методов анализа является – Корреляционный граф, предложенный эстонским математиком Л. Выханду.

Граф – это фигура, состоящая из точек (вершины графа). Примером графа является социограмма, в которой указываются члены группы (вершины графа) и связи между ними (ребра графа). Для построения графа измеряют парные связи между всеми переменными, обозначенными на графе как вершины. Например. Имея пять переменных А, В, С, Д и Е, покажем, как связана каждая из них с каждой другой в матрице интеркорреляции.

	А	В	С	D	Е
A B C D E	1 0,96 0,90 0,01 0,05	0,96 1 0,15 0,85 0,95	0,90 0,15 1 0,02 0,14	0,01 0,85 0,02 1 0,60	0,06 0,95 0,14 0,60 1

Связь между переменными можно описать графом:

B

E

D

A

C

0,96

0,95

0,85

0,60

0,90

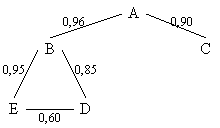Как видно из графа, В и С связаны через А, , поэтому она опущена. Другая связь между ВДЕ. Все они взаимодействуют на уровне R более 0,60. Но каждая из них связана с С очень слабо (0,02 до 0,14).

В корреляционном графе отображаются наиболее тесные связи, а менее тесные связи опускаются.

Другим методом поиска скрытой (латентной) структуры взаимосвязи множества переменных является Факторный анализ. Смысл факторного анализа в том, что принято считать n переменных линейными функциями меньшего числа других переменных, называемых Факторами. Факторы выступают как бы более фундаментальными, обобщенными, переменными, и исходные переменные как бы объединяются в Группы, каждая из которых представляет некий фактор. Задача анализа – найти эти факторы. Поскольку фактор представляет собой объединение переменных, поскольку из этого следует, что эти переменные связаны друг с другом, обладают корреляцией, причем больше между собой, чем с другими переменными, входящими в другой фактор. Методы отыскания факторов основываются на использовании именно коэффициентов корреляции между переменными. Факторный анализ имеет большое значение для характеристики социального явления, поскольку вначале оно характеризовалось n переменными, а в результате применения факторного анализа оказалось, что оно характеризуется меньшим числом – Q других переменных – факторов.

Описательный факторный анализ Дает факторную картину единичного явления, Объясняющий – позволяет найти внутренние глубинные переменные, если применять факторный анализ на разных системах переменных и на разных популяциях.

Процедура факторного анализа предусматривает выполнение нескольких последовательных операций:

1. создание матрицы интеркорреляции путем осуществления парной корреляции всех переменных;

2. последовательное преобразование исходной матрицы и выполнение расчетов направленных на «Извлечение» независимых факторов, характеризующих внутреннюю структуру признакового пространства;

3. поворот осой («Вращение факторов»), которая результатируется в составлении окончательной таблицы данных связей между признаками и факторами;

4. трактовка результатов, каждый из выделяемых факторов получает содержательную характеристику через систему отношений к заданным внешним признакам.

Таким образом, сначала устанавливаются парные корреляции всех изучаемых переменных, а затем описываются «Узлы» связей, то есть выделяют такие переменные, которые, будучи тесно связаны в рамках своей группы, слабо связаны с другими корреляционными узлами. Выявленные «Узлы» и есть факторы.

Для их выявления составляется факторная матрица. Ниже в качестве примера приводится факторная матрица оценок рабочим уровня удовлетворенности различными элементами производственной ситуации (N=4121 опрошенных) по данным исследования, проведенного В. А. Ядовым в Ленинграде в 1976 г.

Оцениваемые элементы Производственной ситуации	Факторные нагрузки
До вращения факторов	После вращения факторов
I	II	I	II
1. Разнообразие работы 2. Важность продукции 3. Возможность проявить смекалку 4. Возможность повышения квалификации 5. Физическая нагрузка 6. Сменность 7. Состояние оборудования 8. Организация труда 9. Ритмичность 10. Санитарно-гигиенические условия 11. Техника безопасности 12. Отношения с администрацией 13. Заработок 14. Отношения с товарищами	0,213 0,352 0,272 0,360 0,275 0,336 0,609 0,707 0,541 0,597 0,653 0,647 0,415 0,410	0,610 0,482 0,696 0,478 0,070 0,134 -0,302 -0,304 -0,249 -0,267 -0,189 -0,052 0,019 0,294	-0,072 0,109 -0,056 0,118 0,236 0,245 0,680 0,771 0,595 0,653 0,670 0,606 0,366 0,242	0,642 0,587 0,745 0,586 0,191 0,266 -0,009 0,026 0,009 0,018 0,112 0,233 0,196 0,443
Общая информативность, «объяснительная сила» фактора (V)	23,4	12,8	21,4	14,8
	36,2	36,2

Из матрицы видно, что первый фактор до вращения вобрал в себя с положительными значениями все изучаемые связи, исчерпав почти четверть их вариации. Это показатель объяснительной «силы» фактора, равной в данном случае 23,4%. Наиболее значимы в этом факторе оценке организации труда (0,707), состояния оборудования (0,609), техники безопасности (0,653), а наименьшие связи обнаруживают оценки содержательных аспектов труда: ее разнообразия (0,213), возможности проявить смекалку (0,272) и т. д. Таким образом, из матрицы видно, что в первом факторе общей удовлетворенности работой лидируют оценки условий труда. Второй фактор, объясняющая сила которого в два раза меньше (12,8%), — биполярный: содержательные аспекты работы вошли в него с положительной оценкой, а условия труда получили отрицательную оценку. Это указание на то, что имеются две подструктуры связей, которые можно прояснить операцией вращения факторов.

После вращения четко обозначились структурные составляющие:

1й фактор (достаточно информативный – 21,4%) – фактор условий труда.

2й фактор – фактор удовлетворенности содержательными аспектами работы.

Далее на основе обнаружения этих двух структур начнем разукрупнять факторную модель на более дробные составляющие, каждому обследованному могут быть приписаны оценки по двух интегральным показателям (двум факторам): удовлетворенности условиями и содержанием труда. Таким образом, вместо 14 исходных показателей получены два обобщенных.