Объектами социологического исследования являются разнообразные множества людей (статистические совокупности) – группы, слои, классы. Совокупности состоят из отдельных единиц – людей или объединений людей. Каждый социальный объект является носителем разнообразных признаков (пол, возраст, образование, отношение к отдельным элементам действительности (к труду, другим людям и т. п.)).
Признаки бывают дискретными (прерывными) и интервальными (непрерывными). Методы статистического анализа эмпирических данных по признакам, представляющим интерес для исследователя, — это способы преобразования информации с целью сделать ее пригодной для проверки рабочих гипотез, интерпретации, получения выводов и практических рекомендаций. В процессе преобразования эмпирических данных различают первичную и вторичную обработку информации.
Первичная обработка заключается в преобразовании исходной информации (ответов респондентов, данных наблюдения и т. п.) путем табулирования, классификации, расчета многомерных распределений и т. д.
Вторичная обработка – преобразование данных первичной обработки – получение показателей, рассчитываемых по частотам, кластерам (например, средние, меры рассеяния, связи, показатели значимости). К вторичной обработке относят такие методы графического представления данных, исходной информацией для которых служат проценты, таблицы, индексы.
Частотой называют числа, показывающие, сколько раз повторяются определенные значения признака в данной совокупности. Отношение соответствующей частоты к объему совокупности называют относительной частотой или Частостью. Последние могут выражаться либо долей, либо в процентах.
Частотное распределение Содержит информацию о том, сколько раз встречается каждое значение признака в изучаемой совокупности. Построение частотного распределения лишь первый этап статистического анализа полученных данных. Следующим шагом является получение обобщающих характеристик, позволяющих глубже понять особенности объекта наблюдения, сравнивая его состояние в разное время или с другими объектами.
К таким обобщающим показателям относятся средние величины (среднее арифметическое, медиана, мода) и меры рассеяния (показатели колеблемости) – вариационный размах, дисперсия, среднее квадратическое отклонение, среднее абсолютное отклонение и т. п.
Среднее арифметическое – частное от деления суммы всех значений признака на их число.
Медиана – значение признака у той единицы совокупности, которая расположена в середине ряда частотного распределения. Если в ряду четное число единиц совокупности (2K), то медиана равна среднему арифметическому из двух серединных значений признака. При нечетном числе единиц совокупности ( ![]() ) медианным будет значение признака у (
) медианным будет значение признака у ( ![]() ) единицы.
) единицы.
В интервальном ряду с различными значениями частот вычисление медианы распадается на два этапа: сначала находят медианный (серединный) интервал, а затем находят значение медианы в пределах этого интервала по формуле:
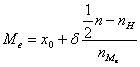 , где
, где
![]() – нижняя граница медианного интервала
– нижняя граница медианного интервала
![]() – величина медианного интервала
– величина медианного интервала
![]() – сумма частот (частостей) интервалов
– сумма частот (частостей) интервалов
![]() – частота (частость), накопленная до медианного интервала.
– частота (частость), накопленная до медианного интервала.
![]() – частота (частость) медианного интервала.
– частота (частость) медианного интервала.
Мода – наиболее часто встречающееся значение признака, то есть значение, с которым наиболее вероятна встреча в данной серии наблюдений. В интервальном ряду (с равными интервалами) модальным является класс с наибольшим числом наблюдений. Значение моды находим в его пределах по формуле:
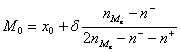 , где
, где
![]() – нижняя граница модального интервала
– нижняя граница модального интервала
![]() – величина модального интервала
– величина модального интервала
![]() – частота интервала предшествующего модальному
– частота интервала предшествующего модальному
![]() – частота интервала, следующего за модальным
– частота интервала, следующего за модальным
![]() – частота модального интервала.
– частота модального интервала.
Степень разброса признаков вокруг средней в ряду распределения характеризуется Показателями колеблемости (рассеяния) данного признака; из них широко используются следующие.
Вариационный размах – разность между крайними значениями (наименьшим и наибольшим) признака в ряду распределения.
Дисперсия – средняя величина квадратов отклонений отдельных значений признаков от средней арифметической:
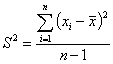 , где
, где
![]() – дисперсия
– дисперсия
N – число значений признака
![]() – отдельное значение признака
– отдельное значение признака
![]() – среднее значение признака
– среднее значение признака
S – корень квадратный из дисперсии называется средним квадратическим отклонением
Среднее абсолютное (линейное) отклонение – среднее арифметическое из абсолютных величин отклонений отдельных значений признака от их среднего арифметического:
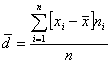 , где
, где
![]() – означает, что суммируются значения отклонений без учета знака этих отношений
– означает, что суммируются значения отклонений без учета знака этих отношений
![]() – объем совокупности
– объем совокупности
Для достаточно большой выборочной совокупности с распределением признака, близкого к нормальному, величина среднего квадратического отклонения всегда больше величины среднего абсолютного отклонения и связана с ним соотношением
![]()
Таким образом, средние величины и показатели колеблемости служат обобщающей характеристикой вариационного ряда значений признака: степени их однородности и разброса.
Применение средних величин не должно носить формальный характер. Ему должен предшествовать качественный анализ объекта, учет целей, задач, гипотез исследования.
