Корреляция выражает такую форму связи, когда определенному значению одной величины соответствует ряд распределения значений другой величины. Так как при корреляционной зависимости каждому X соответствует целый ряд значений Y, то они образуют в системе координат некое «корреляционное поле» величины. Например, более высокой квалификации работников соответствует более высокая зарплата, хотя среди них могут быть люди с разной зарплатой. Корреляционно связаны условия труда и удовлетворенность работой, образование родителей и успеваемость детей, стаж работы и производительность труда. Наличие корреляции свидетельствует о том, что, либо одно из выделенных явлений частичная причина другого, либо оба явления — следствие общих причин. Но выявление корреляции не дает оснований утверждать о причинно — следственной связи явлений. Так, В. Шубкин обнаружил корреляцию между зарплатой родителей и успеваемостью их детей — школьников; Ричардсон между зарплатой учителей и потреблением вин в США. В первом случае корреляция объясняется тем, что, как правило, более образованные родители получали более высокую зарплату, а во втором — тем, что в этот период (1870-1910гг.) в США росла зарплата (в т. ч. и учителей) и соответственно увеличивалось потребление продуктов (в т. ч. и вина), т. е. и зарплата учителей и потребление вина были следствием общих причин, а не причиной и следствием по отношению друг другу.
Показатели, отражающие меру корреляции (тесноту, направление связи) называются коэффициентами корреляции. В социологии применяются коэффициент Юла (Q), коэффициент двусторонней связи (Ф), Пирсона (R), ранговой корреляции Спирмена ( ![]() ), множественный коэффициент корреляции (W), коэффициент Чупрова (Т) и Крамера (К).
), множественный коэффициент корреляции (W), коэффициент Чупрова (Т) и Крамера (К).
Чтобы найти связи между двумя признаками, необходимо составить двухмерную таблицу. Например, нужно установить связь между удовлетворенностью работников профессией Y (Y1 — удовлетворен, Y2 — не удовлетворен) и производительностью труда X (X1 — высокая, X2 — низкая). Пусть из N=100 чел. 50 удовлетворены (Y1=50), а 50 не удовлетворены (Y2=50). Y 20 человек высокая (X1=20), а у 80 низкая (X2=80) производительность труда.
![]()
Обнаружена прямая (функциональная) односторонняя связь между производительностью труда и удовлетворенностью профессией.
Для случая ![]()
![]()
Теперь связи между производительностью труда и удовлетворенностью профессий нет: и у работников с высокой и у работников с низкой производительностью одинаковы числа удовлетворенных и неудовлетворенных профессией.
Q — показатель односторонней связи. Например, если B=0, то Q=1. Это значит, что в исследуемой группе высокая производительность сочетается с удовлетворенностью, но это не означает, что все удовлетворенные профессией характеризуются высокой производительностью.
Построим т. н. корреляционную двумерную таблицу:
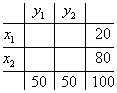
Заполненные внешние клетки называются маргинальными. Но пока мы не знаем распределение респондентов по внутренним клеткам, мы ничего не можем сказать о связи между признаками X и Y. Для удобства обозначим внутриклеточные частоты буквами.
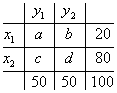
Рассмотрим коэффициент Юла ![]() . Пусть внутриклеточные частоты такие
. Пусть внутриклеточные частоты такие ![]() . Это значит, что все 20 респондентов с высокой производительностью труда (X1) удовлетворены своей профессией (Y1), но не наоборот (среди людей, удовлетворенных профессией (50 чел.) и 30 человек имеют низкую производительность труда).
. Это значит, что все 20 респондентов с высокой производительностью труда (X1) удовлетворены своей профессией (Y1), но не наоборот (среди людей, удовлетворенных профессией (50 чел.) и 30 человек имеют низкую производительность труда).
Q=1 означает обратную связь — высокая производительность соответствует низкой удовлетворенности (в указанном случае). Для описания двусторонней связи используется коэффициент ![]()
Если ![]() обращается в 1, когда хотя бы одна из внутриклеточных частот равна 0, то
обращается в 1, когда хотя бы одна из внутриклеточных частот равна 0, то ![]() =1, если либо A=С=0, либо B=D=0.
=1, если либо A=С=0, либо B=D=0.
Наиболее широко известной мерой корреляции является коэффициент Пирсона (R).
Для расчетов используется двухмерная корреляционная таблица вида (в качестве примера ниже приводится таблица соотношения двух признаков (X) общий стаж работы и зарплата (Y) в группе респондентов 25 человек).
|
№ респондента |
Стаж |
Зарплата |
|
|
|
|
1 2 3 … |
20 21 2 … |
190 180 130 … |
400 441 4 … |
36100 32400 16900 … |
3800 3780 260 … |
|
N=25 |
|
|
|
|
|
![]()
Коэффициент Пирсона 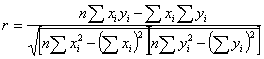
Подставляем данные из таблицы: ![]()
Для проверки статистической значимости полученного коэффициента (не обусловлена ли полученная величина R =0,86 случайностью) при N< 50 применяется критерий T, вычисляемый по формуле ![]() ;
; ![]() .
.
Для случая N>50 используется критерий ![]() . Если полученная (эмпирическая) величина T(Z) больше табличной (критической, ожидаемой), то полученный коэффициент (в нашем примере 0,86 значим с заданной вероятностью
. Если полученная (эмпирическая) величина T(Z) больше табличной (критической, ожидаемой), то полученный коэффициент (в нашем примере 0,86 значим с заданной вероятностью ![]() . если
. если ![]() = 0,01, значит лишь в одном из 100 случаев R=1).
= 0,01, значит лишь в одном из 100 случаев R=1).
Коэффициенты ранговой корреляции Спирмена ( ![]() ), Кендала (
), Кендала ( ![]() ) измеряют взаимосвязь между упорядоченными рядами признаков по степени нарастания или убывания.
) измеряют взаимосвязь между упорядоченными рядами признаков по степени нарастания или убывания.
Коэффициент Спирмена 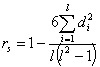 , где
, где
![]() – разность между I-ми парами рангов;
– разность между I-ми парами рангов;
L – число пар рангов
Величина ![]() =1, если оба ряда ранжируются в одном (однонаправленном) порядке (убывания или нарастания).
=1, если оба ряда ранжируются в одном (однонаправленном) порядке (убывания или нарастания). ![]() = -1 при обратной направленности проранжированных рядов.
= -1 при обратной направленности проранжированных рядов. ![]() =0 означает полное взаимное беспорядочное расположение рангов. Для расчетов используется корреляционная таблица вида (в качестве примера приводится таблица о жизненных планах рабочей и крестьянской молодежи).
=0 означает полное взаимное беспорядочное расположение рангов. Для расчетов используется корреляционная таблица вида (в качестве примера приводится таблица о жизненных планах рабочей и крестьянской молодежи).
Жизненные планы |
Социальное происхождение (в %) |
Ранг I |
Ранг II |
|
|
|
|
Из рабочих |
Из крестьян |
|||||
|
Получить высшее образование |
57,5 |
51 |
1 |
3,5 |
-2,5 |
6,25 |
|
Получить интересную работу |
57,3 |
59 |
2 |
1 |
1 |
1 |
|
Побывать в других странах |
53,8 |
52 |
3 |
2 |
1 |
1 |
|
Создать хорошие жилищные условия |
49,7 |
51 |
4 |
3,5 |
0,5 |
0,25 |
|
Материальное благополучие |
48,5 |
50 |
5 |
5 |
5 |
0 |
Значимость коэффициента корреляции для ![]() определяется по таблице критических величин
определяется по таблице критических величин ![]() . Для
. Для ![]() критические значения находятся на необходимом уровне значимости
критические значения находятся на необходимом уровне значимости ![]() по таблице и сравниваются с наблюдаемыми по формуле
по таблице и сравниваются с наблюдаемыми по формуле
![]()
Если Z критическое превышает ZТабл, то можно сделать вывод, что есть значимая связь между ранжированными признаками. В нашем примере между предпочтениями жизненных планов рабочей и крестьянской молодежи.
