Лабораторная работа №7.
Цель работы: — выработать навыки построения корреляционных уравнений вплоть до третьего порядка для выборок малого объема.
1 ОБЩИЕ ПОЛОЖЕНИЯ
1.1 Алгоритм метода двумерного точечного распределения
Метод построения корреляционных и регрессионных уравнений по парным выборкам малого объема основанном на классическом методе Чебышева [5.1;5.2], дополненном методом точечных распределений [5.3]. Рассмотрение алгоритма расчета предлагается начать с числового примера (таблица 7.1).
Таблица 7.1 – Упорядоченная парная выборка объемом n=8
|
Номер измерения, i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Средн. арифм. |
СКО |
|
Хi |
5,32 |
5,97 |
6,06 |
6,20 |
6,70 |
7,33 |
7,61 |
8,01 |
6,65 |
0,9272 |
|
Yi |
38,5 |
41,0 |
41,2 |
42,3 |
47,1 |
50,3 |
51,0 |
51,2 |
45,325 |
5,1558 |
Каждое измерение выборки считается центром виртуального распределения с нормальным законом.
Для создания корреляционной таблицы необходимо первоначально определить границы существования выборок каждого параметра 
и 
, а также интервалов перекрытия каждого ядра 
и 
с одновременным выбором вида ядра, выбором коэффициента 
и количества интервалов дискретности каждого отрезка (a, b), как это предусмотрено алгоритмом для единичной выборки, описанном в [5.3]. При этом опора ведётся на результаты предварительных расчетов по общеизвестным формулам Гаусса для среднего арифметического и Бесселя для среднеквадратических отклонений (СКО), числовые значения которых представлены в таблице 7.1.
Результаты расчетов по алгоритму следующие:
;
; 
; 
Каждый отрезок (a; b) следует разбить на 30 интервалов дискретности и найти центры для каждого интервала. Затем определяется условие накрывания каждой i-ой дельтаобразной функции интервалом задания 
каждого центра j-го интервала дискретности.
Частоты соседних интервалов дискретности следует объединить по три, получаются 10 групп интервалов дискретности. Далее формируется таблица, в столбцах которой располагается центры 10 групп интервалов, а в строках – экспериментальные значения соответствующей выборки. В ячейку, находящуюся на пересечении центра группы и значения рассматриваемой выборки, заносится число, соответствующее условию накрывания интервалов задания для данной выборки. Таким образом формируются таблицы для обеих выборок X и Y (таблицы 7.2 и 7.3).
Таблица 7.2 – Суммарные условные (виртуальные) частоты для выборки
случайной величины Х
|
j |
Xj |
Исходная выборка Xi |
|
|
|
|||||||
|
5,32 |
5,97 |
6,06 |
6,20 |
6,70 |
7,33 |
7,61 |
8,01 |
|||||
|
1 |
4,65 |
1,496 |
0,202 |
0,139 |
0,074 |
0,005 |
1,889 |
8,7839 |
40,8449 |
|||
|
2 |
5,09 |
2,708 |
0,904 |
0,701 |
0,450 |
0,056 |
0,001 |
4,820 |
27,5338 |
124,8770 |
||
|
3 |
5,54 |
2,727 |
2,203 |
1,932 |
1,499 |
0,372 |
0,021 |
0,004 |
8,756 |
48,5193 |
268,7970 |
|
|
4 |
5,98 |
1,500 |
2,930 |
2,904 |
2,727 |
1,335 |
0,183 |
0,051 |
0,005 |
11,653 |
69,5773 |
416,0723 |
|
5 |
6,43 |
0,450 |
2,129 |
2,385 |
2,708 |
2,617 |
0,845 |
0,346 |
0,064 |
11,544 |
74,2279 |
477,2855 |
|
6 |
6,87 |
0,074 |
0,845 |
1,070 |
1,469 |
2,801 |
2,129 |
1,278 |
0,406 |
10,072 |
69,1946 |
475,3672 |
|
7 |
7,32 |
0,006 |
0,183 |
0,262 |
0,435 |
1,637 |
2,930 |
2,572 |
1,410 |
9,435 |
69,0642 |
505,5499 |
|
8 |
7,76 |
0,021 |
0,035 |
0,070 |
0,522 |
2,203 |
2,828 |
2,670 |
8,349 |
64,7882 |
502,7567 |
|
|
9 |
8,21 |
0,001 |
0,003 |
0,006 |
0,091 |
0,904 |
1,699 |
2,761 |
5,465 |
44,8677 |
368,3634 |
|
|
10 |
8,65 |
0,009 |
0,202 |
0,557 |
1,560 |
2,328 |
20,1372 |
174,1868 |
||||
|
|
8,934 |
9,418 |
9,431 |
9,438 |
9,445 |
9,418 |
9,335 |
8,876 |
74,295 |
493,6941 |
3354,1007 |
|
Виртуальное среднее арифметическое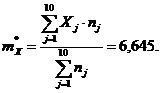 
Виртуальная дисперсия 
Таблица 7.3 – Суммарные условные (виртуальные) частоты для выборки
случайной величины Y
|
l |
Yl |
Исходная выборка Yi |
|
|
|
|||||||
|
38,5 |
41,0 |
41,2 |
42,3 |
47,1 |
50,3 |
51,0 |
51,2 |
|||||
|
1 |
34,19 |
1,171 |
0,296 |
0,258 |
0,113 |
0,001 |
1,839 |
62,8754 |
2149,7103 |
|||
|
2 |
36,66 |
2,481 |
1,158 |
1,061 |
0,610 |
0,013 |
5,232 |
195,1412 |
7153,8757 |
|||
|
3 |
39,14 |
2,873 |
2,470 |
2,376 |
1,789 |
0,128 |
0,006 |
0,003 |
0,002 |
9,647 |
377,5836 |
14778,6213 |
|
4 |
41,61 |
1,817 |
2,877 |
2,906 |
2,863 |
0,664 |
0,070 |
0,038 |
0,031 |
11,266 |
468,7783 |
19505,8634 |
|
5 |
44,09 |
0,627 |
1,931 |
1,942 |
2,503 |
1,873 |
0,436 |
0,276 |
0,241 |
9,729 |
428,9516 |
18912,4765 |
|
6 |
46,56 |
0,118 |
0,636 |
,708 |
1,195 |
2,889 |
1,470 |
1,108 |
1,013 |
9,137 |
425,4187 |
19807,4956 |
|
7 |
49,04 |
0,012 |
0,120 |
0,141 |
0,311 |
2,435 |
2,709 |
2,423 |
2,327 |
10,478 |
513,8411 |
25198,7685 |
|
8 |
51,51 |
0,001 |
0,012 |
0,015 |
0,044 |
1,121 |
2,726 |
2,893 |
2,917 |
9,729 |
501,1408 |
25813,7621 |
|
9 |
53,99 |
0,001 |
0,001 |
0,003 |
0,281 |
1,498 |
1,887 |
1,998 |
5,669 |
306,0693 |
16524,6821 |
|
|
10 |
56,46 |
0,038 |
0,449 |
0,627 |
0,747 |
1,906 |
107,6128 |
6075,8164 |
||||
|
|
9,100 |
9,401 |
9,408 |
9,431 |
9,443 |
9,364 |
9,300 |
9,276 |
74,723 |
3387,4128 |
155921,0719 |
|
Виртуальное среднее арифметическое 
Виртуальная дисперсия 
После того, как были сформированы таблицы для каждой выборки, следует сформировать таблицу двумерного распределения (основа – метод П.Л. Чебышева), клетки которой заполняются по формуле:
(7.1)
где nji, nli – ячейки таблицы 7.2 и таблицы 7.3 соответственно;
n – объем первоначальной парной выборки (в нашем случае 8).
Тогда таблица двумерного распределения будет иметь вид, представленный в таблице 7.4.
Средние арифметические выходной величины 
с учетом разделения по интервалам дискретности выходной величины Xj (строчные средние) подсчитывается по формуле:
а средние средних арифметических
, где 
.
Таблица 7.4 – Таблица двумерного виртуального распределения
|
Xj |
Yl |
nj |
|
|||||||||
|
34,19 |
36,66 |
39,14 |
41,61 |
44,09 |
46,56 |
49,04 |
51,51 |
53,99 |
56,46 |
|||
|
4,65 |
1,8240 |
4,0710 |
5,1810 |
3,8670 |
1,7530 |
0,5010 |
0,0957 |
0,0140 |
0,0018 |
0,0002 |
17,3087 |
39,3695 |
|
5,09 |
3,6710 |
8,7850 |
12,4900 |
10,8800 |
5,9470 |
2,0930 |
0,5210 |
0,1105 |
0,0209 |
0,0029 |
44,5213 |
40,0108 |
|
5,54 |
4,5140 |
12,2900 |
20,6000 |
21,4500 |
13,9500 |
5,9920 |
2,0100 |
0,6123 |
0,1536 |
0,0270 |
81,5989 |
40,9034 |
|
5,98 |
3,6840 |
11,8800 |
23,5000 |
28,3000 |
21,3700 |
11,5400 |
5,5100 |
2,3590 |
0,7705 |
0,1719 |
109,0854 |
41,9979 |
|
6,43 |
2,0820 |
7,8000 |
17,4000 |
23,300 |
20,9700 |
15,5800 |
11,0900 |
6,6060 |
2,7950 |
0,7603 |
108,5133 |
43,6907 |
|
6,87 |
0,7811 |
3,2310 |
7,8430 |
11,9400 |
13,9700 |
16,1100 |
17,3400 |
13,9200 |
7,2070 |
2,2260 |
94,5681 |
46,4970 |
|
7,32 |
0,1798 |
0,7937 |
2,1060 |
3,9730 |
7,3270 |
14,1400 |
21,6300 |
21,4000 |
12,5200 |
4,1600 |
88,2295 |
49,1703 |
|
7,76 |
0,0240 |
0,1134 |
0,3555 |
1,0530 |
3,6440 |
10,7100 |
20,3300 |
22,5600 |
14,1200 |
4,9030 |
77,8129 |
50,3803 |
|
8,20 |
0,0018 |
0,0099 |
0,0481 |
0,3019 |
1,7200 |
6,2800 |
13,2100 |
15,5400 |
10,1000 |
3,6130 |
50,8247 |
50,7760 |
|
8,65 |
0,0001 |
0,0007 |
0,0081 |
0,0904 |
0,6345 |
2,5200 |
5,5480 |
6,7220 |
4,4730 |
1,6300 |
21,6268 |
50,9213 |
|
nl |
16,7618 |
48,9747 |
89,5317 |
105,2853 |
91,2855 |
85,4660 |
97,2847 |
89,8438 |
52,1618 |
17,4943 |
694,0896 |
|
Дисперсия случайной величины может быть подсчитана по формуле
Тогда квадрат корреляционного отношения для приведенного примера равен
.
1.2 Вычисление корреляционных и регрессионных уравнений
классическим методом
П.Л. Чебышев предложил достаточно простой и удобный способ определения уравнений регрессии по найденным моментам различного порядка, корреляционному отношению и коэффициенту корреляции [5.1]. Способ предполагает предварительно найти корреляционное уравнение приближенного условного основного момента 
в виде полинома степени hX
(7.2)
В этом уравнении
Исследование связи между двумя случайными величинами начинается с вычисления смешанных моментов различных порядков. Смешанным центральным моментом порядка (hX, hY) распределения по разрядам совокупно наблюденных значений двух случайных величин X и Y называется выражение вида
. (7.3)
Полагая hY =0 получим 
, то есть центральные моменты порядка hX случайной величины X ; полагая hX=0, получим 
, то есть центральные моменты порядка hY случайной величины Y.
Смешанные основные моменты порядка (hX, hY) находятся при помощи смешанных центральных моментов
. (7.4)
В частности, смешанный основной момент порядка (1,1) r1/1
есть коэффициент корреляции.
Иногда создается парадоксальная, на первый взгляд, ситуация, когда корреляционное отношение велико (то есть факт достаточно тесной связи установлен), а коэффициент корреляции незначим. Это говорит о сугубо нелинейном характере связи, имеющей вид, например, параболы, производная которой в точке экстремума (численно равная коэффициенту корреляции) равна нулю.
В случае, если коэффициент корреляции достаточно велик, правильность вычислений можно установить при подтверждении неравенства 
.
Переход к уравнению регрессии выполняется по формуле
, (7.5)
где 
— вероятное значение величин Y.
Выражение (7.2) является корреляционным уравнением в силу того, что аргументы функции выражены в относительных единицах ξ (в центрированном и нормированном виде). Выражение (7.5) является уравнением регрессии
той же пары, но в абсолютных единицах измерения с учетом среднеквадратических отклонений функции. Именно по этой причине регрессия есть линия – геометрическое место точек проекций центров условных распределений (см. рисунок 7.1).
Выражение (7.2) дает возможность подобрать полином любого (в разумных пределах) порядка, так как построен он следующим образом: для полинома первой степени достаточно принимать в расчет только первый член выражения (7.2), остальными можно пренебречь; для полинома второго порядка два члена и т.д. Показателем того, на каком порядке корреляционного уравнения следует остановиться, служит критерий 
с его основной ошибкой 
. Если величина критерия оказывается достаточно малой (не более двух основных ошибок ), то можно остановиться на корреляционном уравнении hX-го порядка. Если при определенном шаге величина критерия окажется отрицательной, то надо вернуться к уравнению предшествующего порядка.
Критерий линейности вычисляется по формуле
(7.6)
с основной ошибкой 
; критерий квадратичности – по формуле
(7.7)
с основной ошибкой 
; критерий уравнения третьей степени вычисляется по формуле
(7.8)
с основной ошибкой 
.
Поскольку уравнение регрессии есть геометрическое место точек проекций центров условных распределений, то возникает естественный вопрос о границах этих распределений, то есть о границах (коридоре) существования самого уравнения регрессии. Эти границы можно определить как
, (7.9)
где zдов
– квантиль доверительной вероятности Рдов
(обычно Рдов=0,95, тогда zдов-1,96).
Применительно к таблице двумерного виртуального распределения в формулах (7.2) – (7.5) следует все 
заменить на 
, 
заменить на 
, 
— на 
, а 
— на 
.
Тогда по данным таблицы 7.4
и 
.
Критерий линейности (7.6)
с основной ошибкой
.
Так как 
, то искомое уравнение не может быть признано линейным.
Проверим возможность аппроксимации данных таблицы 7.4 уравнением второго порядка
; 
.
; 
.
; 
.
; 
.
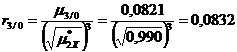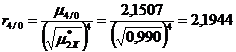Критерий квадратичности (7.7) равен
с основной ошибкой
.
Так как 
, то уравнение не может быть признано квадратичным.
Проверим возможность аппроксимации данных таблицы 7.4 уравнением третьего порядка
; 
.
; 
.
; 
.
;
;
.
Критерий кубичности (7.8) равен
с основной ошибкой 
.
Так как 
, то есть все основания считать, что искомое уравнение имеет третий порядок.
Подставляя в формулу (7.2) найденные числовые значения, имеем
.
Переходя затем к уравнению регрессии (7.5) в именованных величинах, имеем
с коридором существования
.
Графическая интерпретация найденного уравнения регрессии, коридор его существования и экспериментальные данные представлены на рисунке 7.1.
 |
Рисунок 7.1 – Найденное уравнение регрессии, коридор его существования
и экспериментальные данные
1.3 Вычисление с помощью модифицированного индекса Фехнера
Использование классического коэффициента корреляции в качестве меры тесноты линейной связи в виртуальном пространстве выборок малого объема
наталкивается на значительные трудности. Дело в том, что в виртуальном пространстве СКО обеих случайных величин несколько больше по своим числовым значениям, чем СКО исходных выборок, поэтому величина коэффициента корреляции становится заведомо меньше, чем в реальном пространстве (до 1,5 раз). Это может привести к значительно искаженным, а то и вовсе неверным результатам. Кроме того, в реальном пространстве порог достоверности коэффициента корреляции, ниже которого он рассматриваться не может, равен
,
т.е. в диапазоне выборки малого объема n=3÷15 он меняется от rmin=0,752 до rmin=0,545. Дополнительным препятствием для применения коэффициента корреляции является его зависимость от вида закона распределения случайных величин (чем ближе к нормальному, тем достовернее) и от наличия грубых промахов, которые не всегда могут быть выявлены в выборке малого объема.
Мерой тесноты линейной корреляционной связи, свободной от вида закона распределения и даже от наличия некоторого количества грубых промахов, является модифицированный индекс Фехнера (МИФ) [5.2].
Для его определения вместо таблицы двумерного распределения необходимо создать таблицу знаков sign{
} и sign{
}. Если обозначить количество совпадающих знаков через v, а количество несовпадающих – через w (где v+w=N – объем парной выборки, в том числе и в виртуальном пространстве), то МИФ можно определить по формуле
, 7.10)
в которой знаки «плюс» берутся в обоих случаях при v>w, а знаки «минус» — при v<w. МИФ ведет себя так же, как коэффициент корреляции, то есть может меняться в пределах от -1≤f*≤+1, при этом в диапазоне 
и при объемах выборки N>40 практически (с точностью до 5%) совпадает с коэффициентом корреляции. Поэтому МИФ рекомендуется использовать везде, где необходимо установить меру тесноты линейной корреляционной связи (да и само ее наличие) при неясных статистических предпосылках относительно парной выборки.
Решим ту же задачу нахождения корреляционного и регрессионного уравнения с помощью МИФ.
Обращаясь к двумерной таблице 7.4 виртуального распределения можно легко установить, что число совпадающих знаков v=564,601 а число не совпадающих – w=129,489. Для этого достаточно подсчитать суммы njl чисел стоящих в ячейках на пересечении совпадающих и не совпадающих знаков величин X и Y
соответственно.
Тогда величина МИФ согласно формуле (7.10) равна
.
Так как (f*)2=0,7106>η2=0,4825, то критерий ψ1
не может быть определен по формуле (7.6). Другими словами, в этом случае уравнение не может быть найдено выше первого порядка.
Согласно формуле (7.2) корреляционное уравнение запишется в виде
,
а регрессионное уравнение по формуле (7.5) – в виде
(7.11)
с коридором существования
.
Для наглядности графическая интерпретация уравнения (7.12) совмещена с таким же представлением уравнения (7.10) на рисунке 7.1. Сравнение их друг с другом приводит к выводам, что оба уравнения имеют право на существование и удовлетворяют исходной выборке малого объема, однако коридор существования уравнения (7.12) меньше (примерно 25%) такого же коридора существования уравнения (7.10) и, следовательно, уравнения (7.12) является более точным.
2 ПОРЯДОК ПРОВЕДЕНИЯ РАБОТЫ
2.1 По таблице исходных данных к лабораторной работе № 4 (таблица 4.1) выписать парную выборку X – Y малого объема (из трех факторов X1, X2, X3 в эту выборку можно взять тот фактор, который использовался в лабораторной работе № 6 – это уменьшит объем дальнейшей расчетной работы).
2.2 Рассчитать границы (a, b) существования выборок каждой случайной величины X и Y и определить интервалы ±ρ
перекрытия их ядер.
2.3 Для k=30 интервалов дискретности по каждой случайной величине X и Y определить центры интервалов дискретности и построить таблицы суммарных условных (виртуальных) частот, подобных таблицам 7.2 и 7.3 (таблицу для случайной величины X можно перенести из лабораторной работы № 6).
2.4 По формуле (7.1) создать таблицу двумерного виртуального распределения, подобную таблицу 7.4, и определить строчные суммы и строчные средние арифметические величины .
2.5 Рассчитать среднее средних и дисперсию 
строчных значений и определить квадрат корреляционного отношения η2.
2.6 Определить число совпадающих v и не совпадающих w знаков таблицы двумерного распределения и рассчитать модифицированный индекс Фехнера (МИФ) f*.
2.7 Если η2 ≥(f*)2 , то дальнейший поиск уравнения регрессии вести по алгоритму раздела 2.1, заменив в расчетах коэффициент корреляции r1/1 на МИФ f*.
Если η2<(f*)2, то следует ограничиться регрессионным уравнением первого порядка и расчет его вести по алгоритму раздела 1.3.
2.8 Полученное регрессионное уравнение изобразить графически с указанием коридора его существования и в тех же координатах найти все точки исходного парного распределения малого объема.
2.9 Сделать выводы из проделанной работы.
3 СОДЕРЖАНИЕ ОТЧЕТА
Отчет о лабораторной работе должен содержать таблицу исходной парной выборки X-Y малого объема, таблицы суммарных виртуальных частот для каждой случайной величины, таблицу двумерного распределения, подробную запись промежуточных и окончательных расчетов при поиске корреляционной и регрессионной моделей, а также графическое представление последней.
При подготовке к защите лабораторной работы необходимо ознакомиться с контрольными вопросами и продумать ответы на них.
4 КОНТРОЛЬНЫЕ ВОПРОСЫ
4.1 Какое уравнение можно назвать корреляционным?
4.2 Какое уравнение можно назвать регрессионным?
4.3 В чем отличия корреляционных и регрессионных уравнений друг от друга?
4.4 Зачем нужны таблицы суммарных виртуальных частот каждой случайной величины?
4.5 Зачем нужна таблица двумерного виртуального распределения?
4.6 Как находятся частоты njl
на пересечении строк и столбцов таблицы двумерного виртуального распределения?
4.7 Как рассчитывается величина квадрата корреляционного отношения?
4.8 Что такое модифицированный индекс Фехнера (МИФ)? Какими достоинствами и недостатками он обладает?
4.9 Каков общий алгоритм расчета регрессионного уравнения hx порядка?
4.10 В каких случаях следует искать уравнение регрессии порядка hx>1, а в каких следует ограничиться только уравнением первого порядка?
4.11 Какие уравнения регрессии, найденные с использованием различных мер тесноты линейной связи, являются более точными? Почему?
5 РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
5.1 Митропольский А.К. Техника статистических вычислений. – 2-е изд., перераб. и доп. – М.: Наука, 1971. – 576 с.
5.2 Долгов Ю.А. Статистическое моделирование. — Тирасполь: РИО ПГУ, 2002. – 280 с. (c. 39-44).
5.3 Метод повышения точности вычисления параметров выборки малого объема // Настоящее учебное пособие. Лабораторная работа № 6.
5.4 Столяренко Ю.А. Корреляция по выборкам малого объема // МНТК Информационные технологии в науке, технике и образовании. Аланья — Севастополь, май – сентябрь 2004 г., С. 110
