Ответ 320.1.

Пусть N=10x+y делится на 7. Тогда

10х + у = 7к,

где к — целое положительное число. Число, обращенное и увеличенное на цифру десятков данного числа, имеет вид:

Подставим сюда 7к—10х вместо у, получим число: 10 (7k—10х)+2х—70k—98х, которое, как видно, делится на 7.

Ответ 320.2.
 Пусть
 делится на 7. Тогда
, где к — целое положительное число.

Число, обращенное и уменьшенное на разность цифр единиц и сотен данного числа, имеет вид:

Заменим здесь z через
; получим число:

которое, как видно, делится на 7.

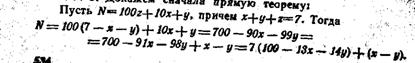
Ответ 320.3.

Докажем сначала прямую теорему: Пусть

Для того чтобы N делилось на 7, необходимо, чтобы х—у делилось на 7. Так как, по условию, х<7 и у<7, то это может быть лишь при

Прямая теорема говорит, следовательно, о необходимом условии делимости числа N на 7.

Докажем теперь обратную теорему. Пусть

причем х=у. Тогда

Как видно, оно делится на 7. Обратная теорема говорит, следовательно, о достаточном условии делимости числа на 7.