Ответ 296.2.
Пусть ваш друг задумал число я, а вы — число р. Произведя с тем и другим числом ряд одинаковых умножений и делений, получаем результаты такого вида:
Оба эти результата, разделенные первый на л, а второй на р, дадут, очевидно, одно и то же число:
Зная это число и сумму
достаточно из последней вычесть первое, чтобы получить число n.
Ответ 296.3.
Случай 1. Задуманное число имеет вид 4n. Произведем требуемые действия:
(остатка нет). Задуманное число 4n.
Случай 2. Задуманное число имеет вид
. Его большая часть
Имеем:
Остаток меньше пяти. Задуманное число 4n+1.
Случай 3. Задуманное число имеет вид
. Имеем:
Прибавляя к этому результату его большую часть, то есть
, получаем:
Остаток равен пяти. Задуманное число 4n+2.
Случай 4. Задуманное число имеет вид 4n+3. Его большая часть
. Имеем:
Его большая часть
, поэтому
Остаток больше пяти. Задуманное число 4n+3.
Ответ 296.4.
Очевидно, что если задумано число вида 4n, где n=0, 1, 2, 3,…, то окончательный результат вычислений дает 5л, то есть число, кратное девяти. Следовательно, сумма цифр этого числа должна делиться на 9, а это значит, что утаенная цифра дополняет сумму оставшихся до числа, кратного девяти. Если же сумма известных цифр сама кратна девяти, то значит, скрытая цифра 9 или 0, но нулем она не может быть по условию.
Для чисел вида
результат вычислений дает соответственно:
. Сумма цифр этих чисел становится кратной девяти только после прибавления в первом случае 6, во втором 4 и в третьем 1.
Значит, и в этих случаях скрытая цифра должна дополнять сумму оставшихся до числа, кратного девяти.
Ответ 296.5.
Обозначим задуманное число буквой х, а прибавляемое — буквой у. Выполняя требуемые действия, получим:
Отсюда видно, что задуманное число (х) равно половине результата
, деленной на прибаиленное число (у) минус половина делителя
Ответ 296.6.
Обозначим задуманное число буквой х, частные от деления на 3, 4 и 5 соответственно буквами а, Ь и с, а остатки буквами r1, r2 и r3. Имеем три очевидных тождества:
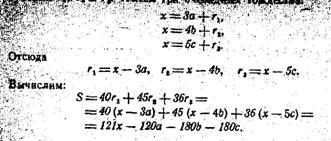
Множители 40, 45 и 56 так и были подобраны, что все члены получившейся алгебраической суммы делятся без остатка на 60, кроме первого (121 х), который при делении на 60 как раз и дает остаток, равный задуманному числу х. Справедливость правила доказана.
Ответ 297.1.
Ответ 297.1.
Действия, которые в данном случае производятся над задуманным числом n, можно выразить так:
, а это выражение представить в виде
. Ясно, что, вычитая
, получим остаток
Замечание. Всегда можно подобрать такие числа, чтобы дробей не получалось.
2. Обозначим буквой х число, заранее написанное вами, а буквой у — число, написанное участником фокуса. Первое действие, выполненное участником, приводит к числу у+99—х. Так как, по условию, х не более 50, а у — в пределах от 51 до 100, то у+99—х не меньше 100, но и не больше чем 199, то есть непременно трехзначное число, цифра сотен которого 1. Зачеркнуть в таком числе 1 — это значит уменьшить его на 100; поэтому второе действие, выполненное участником, приводит к числу y + 99 – x—100 + 1= y—x. Последнее действие, y— (y—x)=x, приводит к числу х, что и требовалось доказать.
Замечание. Вы можете разрешить участникам фокуса задумывать числа в другом диапазоне, например между 201 и 1000, но тогда и спрятанное число должно быть не меньше 100 и не больше 200, а в дальнейших расчетах должно употребляться число 999 вместо 99.
