В начале XIII века в городе Пизе (Италия) жил большой знаток всевозможных соотношений между числами и весьма искусный вычислитель Леонардо (с добавлением к его имени Пизанский). Его звали еще Фибоначчи, что значит сын Боначчи. В 1202 г. он издал книгу на латинском языке под названием Книга об абаке (Incipit Liber, Abbaci compositus a Leonardo filius Bonacci Pisano), содержащую в себе всю совокупность знаний того времени по арифметике и алгебре. Это была одна из первых книг в Европе, учившая употреблять десятичную систему счисления. Книга Леонардо Пизанского получила широкое распространение и более двух веков являлась наиболее авторитетным источником знаний в области чисел.
По обычаям того времени Фибоначчи участвовал в математических турнирах (публичное состязание в наилучшем и наиболее быстром решении трудных задач; нечто вроде наших математических олимпиад). Леонардово искусство в решении числовых задач изумляло всех.
Высокая репутация Фибоначчи привлекла однажды (в 1225 г.) в Пизу государя Римской империи Фридриха II, который приехал в сопровождении группы математиков, желавших публично испытать Леонардо. Одна из задач, предложенных на турнире, имела следующее содержание:
Найти полный квадрат, остающийся полным квадратом как после увеличения его, так и после уменьшения на 5.
Напомню, что полным квадратом называется число, из которого точно извлекается квадратный корень.
Фибоначчи после некоторых размышлений нашел такое число. Оно оказалось дробным;
Действительно,
иначе
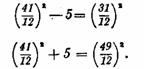
Какими соображениями руководствовался Фибоначчи во время турнира, этого мы не знаем, но задачу он решил блестяще.
В книге Г. Н. Попова Исторические задачи (ОНТИ, 1932 г.) приведено такое решение этой задачи: по условию,
Отсюда
Но
значит,
Полагая
получаем
а затем и
Может быть Фибоначчи, действительно, так и решал задачу на турнире; в таком случае какой же силой числового воображения надо обладать, чтобы догадаться заменить 10 дробью
Такая догадка кажется невероятной, тем более в условиях турнира. Возможно, что приведенное решение является лишь продуктом более поздней обработки процесса размышлений?
Так или иначе, но уже с первого издания Математической смекалки эта задача вызвала большой творческий Отклик со стороны любителей математики. Начались поиски наилучшего решения; возникло желание выяснить, для каких иных натуральных чисел, заданных вместо числа 5, можно поставить и решить аналогичную задачу.
В этих поисках, пожалуй, больше других продвинулся инж. Н. В. Никифоров (Пермь), решение которого далее и воспроизводится с небольшими изменениями.
Пусть искомое число —дробь вида
а величина его изменения — г (г=5 — частный случай )). Имеем,
|
|
где, по условию,
также полные квадаты. Обозначим
Складывая (1) и (2), найдем, что
Подставив полученное выражение в (1) или (2), получим еще одну формулу, которую можно представить в следующем виде:
Замечаем, что b > а, а также, что числа
образуют арифметическую прогрессию с разностью d = (b –a) /2. Произвольно назначая числовые значения для а и b (b > а), определяем по формуле (4) подходящие значения г и у, а затем по формуле (3) находим х.
Естественнее всего взять прогрессию из натуральных чисел со знаменателем d = 1. Тогда если а = n—1, где n — натуральное число, то формулы (4) и (3) принимают такой вид:
(n – 1)n(n + 1) = ry2 (5)
X = (n2 + 1)/2 (6)
Пусть n = 2. Левая часть формулы (5) становится числом 1 ∙ 2 ∙ 3. Запишем его как 6 ∙ 12. Сравнивая это число с правой частью формулы (5), заключаем, что r = 6, y = 1. По формуле (6) находим x =5/2. В результате получаем, что число
—это такой полный квадрат, который остается полным квадратом после увеличения и после уменьшения его на
Пусть n = 7. Левая часть формулы (5) становится числом
Запишем его как
. Сравнивая это число с правой частью формулы (5), заключаем, что
. По формуле (б) находим х=25. Значит, 121 остается полным квадратом после изменения его на ±21.
Как видим, придавая n в формуле (5) любое значение, большее единицы, всегда можно найти такое г и такое искомое число —
для которых задача может быть поставлена и решена (нужно еще, чтобы было
). Понятно, что если формула (5) будет иметь место при разных n и у, но одном и том же r, то и искомых чисел будет несколько при одном заданном r. Так, например, при r = 6
искомым числом будет не только
но и
. Это число получается по формулам (5) и (6) при n = 49.
Если r=5 (как в задаче Фибоначчи), то соответствующее число (41/12)2 получается по формулам (5) и (6) при
п=9. Фибоначчи не дал других ответов для турнирной задачи (г=5), а они, несомненно, должны быть. Формулы Н. В. Никифорова позволяют легко обосновать весьма любопытное положение: если для заданного r найдено число, удовлетворяющее условию, то это число служит источником для получения любого количества других решений той же задачи. Покажем это на примере найденного решения турнирной задачи. Имеем три числа:
Ясно, что
образуют прогрессию с разностью 5, значит, эти числа сами могут быть значениями
для формулы (4). Так как, кроме того,
и r = 5, то формула (4) обеспечивает рациональное значение для у, а следовательно, еще один искомый ответ. В самом деле, по формуле (4)
откуда
По формуле (3)
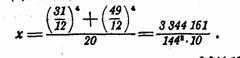
Выполняя деление х на у, получаем
Число
и будет вторым ответом на турнирную задачу (В первом издании Математической смекалки это число ошибочно было дано как первая степень искомого числа. В последующих изданиях оно не приводилось совсем). В этом случае
Последние два квадратных числа можно вновь принять в качестве а и b для формул (4) и (3) — получится третий ответ для турнирной задачи:
и т. д.
Для самостоятельного решения (без ответов): Задана 1. Покажите, что при
формулы (3) и (4) обращаются в следующие тождества:
Придавая г произвольные значения, вы получите условия и решения разнообразных задач, аналогичных турнирной.
Задача 2. Справедливо ли утверждение, что при r = 7 турнирная задача не имела бы решения в области рациональных чисел?
