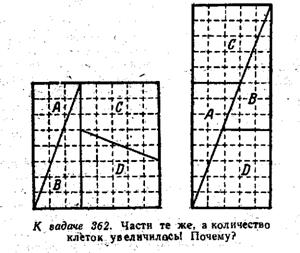
С числами Фибоначчи косвенно связан занятный геометрический парадокс.

Совершенно очевидно, что если какую-либо плоскую фигуру разрезать на несколько частей, затем, прикладывая полученные части друг к другу (но не накладывая одну на другую), образовать новую фигуру, то по форме новая фигура может отличаться от первоначальной, но площадь ее должна остаться прежней; ни одной квадратной единицы не может ни прибавиться, ни убавиться. Это очевидное утверждение считается в геометрии одним из тех первичных основных положений, на которых строится вся теория измерения площадей.

На рисунке показано превращение квадрата в прямоугольник.

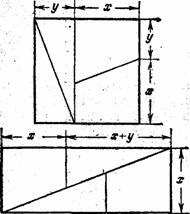
Квадрат разрезан на два равных треугольника и на две равные трапеции, длины сторон которых пока обозначены буквами х и у. Из этих частей составлен прямоугольник. Если такое превращение квадрата в прямоугольник действительно возможно, то на какие же части х и у надо при этом делить сторону квадрата?

Один мой юный друг решил установить это практически и натолкнулся при этом на поразительное явление.

— Дай, думаю, — пишет он в письме,— я сам проделаю это превращение практически. Копировать рисунок с книги мне не хотелось. Я решил сам разметить свой квадрат, пользуясь указаниями рисунка. Нарисовал я на клетчатой бумаге квадрат в 64 клетки и задумался над вопросом: на какие части х и у разделить сторону квадрата. Сначала я подумал, что это безразлично, и положил х=6, у=2. Разметил квадрат, разрезал его на два равных треугольника и две равные трапеции, начал составлять прямоугольник, как указано на рисунке и … ничего не вышло! Сплошного прямоугольника не получилось. Не получался сплошной прямоугольник и при других значениях х и у, например при
.

Только при х=5, 1=3 я смог составить прямоугольник из образовавшихся частей квадрата, но тут же был ошеломлен новой неприятностью: площадь прямоугольника оказалась равной 65 клеткам, то есть на одну клетку большей, чем площадь первоначально взятого квадрата мок ниже).

В самом деле, судя по рисунку на предыдущей странице, длина прямоугольника должна содержать x + x + y =
единиц; у меня и получилось ровно 13 единиц; ширина прямоугольника х, и у меня получилась ширина прямоугольника 5 единиц (рисунок на этой странице). Отсюда его площадь содержит ровно
 клеток! Проделайте сами!

Но это еще не все. По той же выкройке (см. рисунок на стр. 372) я делил на части и другой квадрат со стороной в 13 единиц. Если я брал
 то из частей квадрата складывался прямоугольник, но … в этот раз с площадью, меньшей площади квадрата, причем тоже ровно

на 1 клетку.

Судите сами: площадь квадрата содержит 13²=169 клеток, а площадь прямоугольника содержит

Еще два примера:

1. Беру квадрат в 21×21=441 клетку. Делю сторону на Части х=13, у=8. Разрезаю. Складываю.

Прямоугольник получается. Подсчитываю площадь:

Опять лишняя клетка.

2. Беру квадрат в 34×34=1156 клеток. Делю сторону на части x=21, у =13. Разрезаю. Складываю. Прямоугольник получается. Подсчитываю площадь:

Не хватает одной клетки!

Что за притча?! Почему так получается?

Что бы вы ответили моему юному другу? Обдумайте хорошенько весь этот парадокс, прежде чем прочтете решение. Какую роль в нем играют числа Фибоначчи?