Обнаружено много интересных соотношений между числами ряда Фибоначчи:
1, 1, 2, 3, 5, 8, 13, 21, …
1. Принцип образования членов этого ряда приводит к следующему соотношению методу любыми его тремя рядом стоящими членами
Эта формула дает возможность по первым двум членам ряда установить его третий член, по второму и третьему— четвертый, по третьему и четвертому — пятый
и т. д.
2. Интересно было бы уметь сразу получить любой член ряда
, зная лишь номер n его места. Оказывается, это вполне возможно, но здесь мы столкнемся с одной из удивительных неожиданностей, которые нередки в математике.
Любой член ряда Фибоначчи — число целое, номер места — тоже число целое. Естественно было бы ожидать, что любой член ряда
получается в зависимости от номера n занимаемого им места при помощи действий только над целыми числами (например, как в прогрессиях). Но это не так. Не только целые числа, но даже все целые и дробные (рациональные) бессильны образовать интересующую нас формулу.
Из затруднительного положения помогают выйти два иррациональных числа:
Вспомните, как эти же два числа обращали в нуль разность R между площадями прямоугольника и квадрата (см решение к задаче №362 на стр. 555). Поистине неожиданная встреча!
Так вот, если n — номер места, то любой член
ряда Фибоначчи вы можете получить по формуле
Так как для двух соседних членов ряда эта формула подтверждается, а всякий последующий член ряда Фибоначчи получается как сумма двух предыдущих, то далее нет надобности проверять справедливость формулы для отдельных случаев; можно сразу убедиться в ее справедливости для любого номера n. Напишем ее выражение для двух соседних n:
Формула (1) будет справедлива для любого n, если сумма этих двух выражений даст соответствующее выражение для
:
|
|
Зная, что представляют собой а1
и а2, вы легко можете проверить расчетом, что
Возвращаясь к сумме
получим:
что и требовалось доказать.
3. Зная, как любой член
ряда Фибоначчи определяется по номеру n занимаемого им места:
легко доказать, что любая пара соседних чисел ряда Фибоначчи
удовлетворяет одному из уравнений
причем, если
Заменяя неизвестные уравнения соответствующими выражениями
Следовательно, при n четном
а при n нечетном
4. Очень забавный вид у формулы для суммы n членов ряда Фибоначчи:
Сумма n первых членов ряда Фибоначчи на 1 меньше (n + 2)-го члена того же ряда.
Доказательство. По закону образования членов ряда имеем:
Складывая эти равенства и уничтожая подобные члены, получим:
5. Сумма квадратов чисел ряда Фибоначчи выражается через произведение двух соседних членов того же ряда:
Для доказательства применим метод полной математической индукции. Пусть формула (2) верна для некоторого числа членов k:
Прибавим к обеим частям равенства по
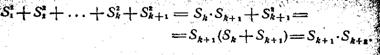
Формула, справедливая, по предположению, для к слагаемых, осталась справедливой и для k+1 слагаемых.
Как показала непосредственная проверка, формула (2) справедлива для k=2. Этого достаточно, чтобы теперь утверждать, что она будет справедливой и для любого целого числа п.
Используя формулу (1) или метод полной математической индукции, докажите самостоятельно еще следующие соотношения.
6. Квадрат каждого члена ряда Фибоначчи, уменьшенный на произведение предшествующего и последующего членов, дает попеременно то +1, то —1.
Например,
10. В ряду Фибоначчи каждое третье число четное, каждое четвертое делится на 3, каждое пятое — на 5, каждое пятнадцатое — на 10.
11. Невозможно построить треугольник, сторонами которого являются числа ряда Фибоначчи (предполагается, что никакое число ряда не может быть употреблено дважды).
12. Если взять любые 4 последовательных числа ряда Фибоначчи и рассматривать произведение крайних членов и удвоенное произведение средних как длины катетов прямоугольного треугольника, то длиной его гипотенузы т один из членов этого ряда:
Дополнительные сведения о свойствах чисел Фибоначчи имеются в книге Н. Н. Воробьева, Числа Фибоначчи, Гостехиздат, 1951. Числовым рядам, аналогичным ряду Фибоначчи, посвящена книга А. И. Маркушевича, Возвратные последовательности, Гостехиздат, 1950.
