1. Еще задолго до нашей эры ученые, комбинируя натуральные числа, составляли из них затейливые ряды,
Придавая элементам этих рядов то или иное геометрическое истолкование.
Так, например, в V — IV веках до н. э. возникли представления о рядах так называемых фигурных чисел.
Рассмотрим сначала такой ряд, в котором разность между каждым последующим и предыдущим членами равна одному и тому же натуральному числу (арифметическая прогрессия), например
1, 2, 3, 4, 5, … (разность d=1),
1, 3, 5, 7, 9, … (разность d = 2),
1, 4, 7, 10, 13, … (разность d = 3);
или в общем виде:
У каждого элемента ряда есть свое место. Чтобы получить n-й элемент ряда (назовем его аn), надо к первому элементу ряда прибавить произведение разности ряда на число, которое на 1 меньше номера места, занимаемого этим элементом аn:
Элементы каждого из таких рядов называются линейными фигурными числами, или, иначе, фигурными числами первого порядка.
2. Из рядов с линейными фигурными числами образуем последовательные суммы этих чисел: первую «сумму» из одного первого элемента ряда линейных фигурных числе, вторую сумму – складывая первые два элемента тоже ряда, третью сумму — складывая первые три элемента и т. д., n-ю сумму — складывая первые nэлементов.
Так, первый ряд линейных фигурных чисел
1, 2, 3, 4, 5, …
Производит следующий новый ряд, ряд сумм:
Назвали эти числа треугольными.
Второй ряд линейных фигурных чисел
1, 4, 9, 16, 25,..
Эти числа назвали квадратными.
Из третьего ряда линейных фигурных чисел
1, 4, 7, 10, 13,…
можно произвести ряд пятиугольных чисел
1, 5, 12, 22, 35,…
Аналогично можно образовать шестиугольные, семиугольные и
т. п. числа. t‘
Все эти многоугольные числа называются плоскими фигурными числами, или фигурными числами второго порядка.
3. Геометрические «имена», которые получили эти числа, объясняются возможностью дать им наглядное истолкование. Построим равносторонний треугольник, квадрат, правильные пятиугольник, шестиугольник и т. д.
со сторонами, равными 1. Затем, отправляясь в каждой фигуре от одной из вершин, удлиним все стороны в 2, 3, 4,… раз, то есть, как говорят математики, построим многоугольники перспективно-подобные данным (см. рисунок на следующей странице).
Во всех вершинах получившихся фигур и на их сторонах на расстояниях, равных 1, поместим кружочки.
К задаче 364. Фигурные числа.
Подсчет кружочков, расположенных в каждом треугольнике, приводит к ряду треугольных чисел
1, 3, 6, 10, 15, …
Подсчет кружочков, расположенных в каждом треугольнике, приводит к ряду треугольных чисел
1, 3, 6, 10, 15, …
Подсчет кружочков, расположенных в каждом квадрате, дает последовательность квадратных чисел
1, 4, 9, 16, 25, …
Аналогичные подсчеты кружочков в каждом пятиугольнике, шестиугольнике и т. д. приводят к последовательностям чисел пятиугольных, шестиугольных и т. д.
4. Дадим сводку всех плоских фигурных чисел:
Общий член Sn каждого ряда плоских фигурных чисел, как это следует из их определения, представляет собой сумму n элементов соответствующего ряда линейных 1 фигурных чисел:
Другими словами, Sn — это сумма n членов арифметической прогрессии, у которой
и разность d=1, 2, 3, … Вспомните формулу для суммы членов арифметической прогрессии:
По этой формуле имеем
Отсюда при d=1 получаем формулу для Sn первой строки таблицы, при
получаем формулу для Sn второй строки таблицы и т. д.
5. Между натуральными числами и плоскими фигурными числами и между самими плоскими фигурными числами существует много любопытных зависимостей.
Пьер Ферма (1601—1665), юрист и общественный деятель города Тулузы (Франция), занимавшийся математикой в часы досуга, что, однако, не помешало ему сделать крупнейшие открытия в теории чисел, обнаружил, например, что
а) всякое натуральное число есть треугольное, или сумма двух или трех треугольных чисел;
б) всякое натуральное число есть или квадрат, или сумма двух, трех или четырех квадратных чисел; всякое
натуральное число есть или пятиугольное, или сумма двух, трех, четырех или пяти пятиугольных чисел;
в) вообще всякое натуральное число может быть представлено в виде суммы не более чем k k-угольных
чисел.
Для отдельных частных случаев эту теорему доказал Эйлер, а общее доказательство дал в 1815 г. французский математик Коши.
Поупражняйтесь: возьмите какое-нибудь натуральное число и разложите его на сумму треугольных, квадратных или пятиугольных чисел. Можно соревноваться, кто быстрее сделает.
(>. Математик Диофант (Греция, III век до н. э.) ел простую связь между треугольными числами T и квадратными K:
8Т + 1 = К.
Можно очень наглядно представить себе эту формулу Диофанта хотя бы на примере треугольного числа 21.
На рисунке изображено 169 пятнышек, которые размещены в квадрате. Они образуют квадратное число K. Одно пятнышко нанимает центр квадрата, и остальные 168 сгруппированы в 8 треугольных чисел Т в форме восьми «прямоугольных треугольников» с ломаными гипотенузами.
Получается: 8Т+1=К
7. В качестве самостоятельного упражнения докажите алгебраически:
а) справедливость формулы Диофанта,
б) что никакое треугольное число не может оканчиваться цифрами 2, 4, 7 и 9.
в) что всякое шестиугольное число есть треугольное с нечетным номером.
8. Для суммы степеней натуральных чисел, то есть одного из видов линейных фигурных чисел, известна
такая формула:
Якоби нашел другую интересную зависимость между теми же числами:
Аналогичная зависимость обнаружена между суммами степеней треугольных чисел, то есть одного из видов
плоских фигурных чисел:
9. Составляя последовательные суммы из плоских фигурных чисел
и т. д., получим пространственные фигурные числа, или фигурные числа третьего порядка: V1, V2 V3, …
Так, ряд треугольных чисел
1, 3, 6, 10, 15, …
производит следующий ряд фигурных чисел третьего порядка:
1, 4, 10, 20, 35, …
Эти числа называют еще пирамидальными, так как для их геометрического представления выкладываются пирамиды из шаров одинакового диаметра.
^
К задаче 364.
Подложим под шар три шара. Получим «пирамиду» из четырех шаров как изображение числа 4. Подложим снизу еще 6 шаров, получим пирамиду из 10 шаров как изображение числа 10 и т. д.
10. Дадим сводку всех фигурных чисел третьего порядка:
Вывести формулу общего члена Vn для пространственных фигурных чисел труднее, чем для плоских. Потребуются некоторые знания из теории соединений. Те из читателей, кто теории соединений еще не изучал, могут пропустить дальнейшее изложение вывода формул для Vn.
Введем обозначения:
Замечаем, что коэффициенты при b1 и r1 могут быть выражены формулами сочетаний из двух элементов:
Подставляя сюда выражения для b1, r1 и раскрывая формулы сочетаний, получим:
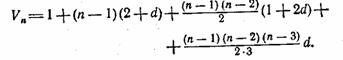
После преобразований
(см. первую и вторую строки таблицы на стр. 385).
11. Тема для самостоятельных упражнений (только для тех, кто знает формулы и свойства «сочетаний»):
Таким же путем, как были получены фигурные числа третьего порядка, образуйте фигурные числа четвертого
порядка и найдите формулу общего члена.
