Опыт 1. Напишем подряд четыре произвольных целых положительных числа, например 8, 17, 3, 107. Вычислим ; разности между первым и вторым числами (вычитая из большего числа меньшее), между вторым и третьим, между третьим и четвертым, наконец, между четвертым и первым, каждый раз вычитая из большего числа меньшее:

17—8=9, 17—3=14, 107–3=104, 107—8=99.

Назовем полученные разности первыми и расположим их по порядку в ряд: 9, 14, 104, 99.

Опять вычислим разности между первым и вторым, вторым и третьим, третьим и четвертым, четвертым и первым числами ряда первых разностей, каждый раз вычитая из большего числа меньшее:

14—9=5, 104—14=90, 104—99=5, 99–9=90. Получим ряд вторых разностей: 5, 90, 5, 90.

Таким же образом составим ряд третьих разностей:

85, 85, 85, 85.

Ну, а ряд четвертых разностей будет состоять из одних нулей: 0, 0, 0, 0.

Повторим опыт с другой группой чисел. Введем обозначения: А₀ — для начальной группы чисел, A₁— для группы первых разностей, А₂ —для группы вторых разностей и т. д.

Пусть начальная группа А₀
содержит следующие четыре числа:

(93, 5, 21, 50).

Выполняем действия:

Сделав всего лишь семь шагов, мы опять пришли к группе нулей.

Экспериментатор должен разнообразить условия опыта. Повторим опыт на какой-нибудь широко растянутой четверке чисел, например, на числах: 1, 11, 130, 1760:

Нули получились и, против ожидания, довольно скоро, в шесть шагов!

Проделайте сами еще десяток таких испытаний над различными группами из четырех целых положительных чисел; в любом случае вы дойдете до группы нулей, причем чаще всего (но не всегда) не более чем за 8 шагов.

Закономерно ли наблюдаемое явление или, может быть, найдется такая четверка чисел, которую не удастся довести до нулей, сколько бы разностей мы ни образовывали? Выяснить это нелегко. Потребуется некоторая изобретательность в построении необходимой цепочки рассуждений. Все-таки надо попытаться. Поиски решения полезны даже и в том случае, когда не удается самостоятельно добраться до полного решения.

Замечание 1. Таким же свойством обращаться в нули обладают последовательные разности любой группы из восьми чисел или из 16 и вообще из 2ⁿ
чисел n — любое целое положительное число).

Замечание 2. Если количество чисел в исходной группе не есть степень 2 (то есть не 4, не 8, не 16 и т. д.), то процесс составления разностей может и никогда не привести к ряду нулей. Например, пусть А₀=(2, 5, 9), тогда

A₈ совпало с A₅, следовательно дальше будут без конца повторяться разности A₆, A₇, A₈.

Опыт 2. Напишите любое целое число и сложите квадраты его цифр. У получившегося результата снова сложите квадраты цифр. Повторяя эту операцию некоторое число раз, вы непременно придете или к числу 1, или к числу 89. Так, например, для числа 31 имеем:

3² + 1² = 10

1² + 0² = 1

К такому же результату, очевидно, сразу приведут числа вида 10ⁿ ,
где n— любое целое число, а также числа, составленные из цифр 1 и 3, или 6 и 8, взятых по одному разу, и любого количества нулей, то есть такие, например, как 13, 103, 3001, 68, 608, 8006 и т. п.

Возьмем теперь какое-нибудь другое число, например 48. В этом случае

Продолжая операцию, получим:

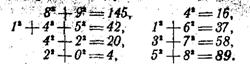
На восьмом шагу повторилось число 89. Замечаем, что промежуточными числами были 145, 42, 20, 4, 16, 37 и 58. Отсюда следует, что если действительно сумма квадратов цифр любого числа в конце концов приводит к числу 1 или к числу 89, то в последнем случае окончательную сумму можно довести при желании не до 89, а до любого из 7 чисел: 145, 42, 20, 4, 16, 37 или 58.

Произведите сами еще несколько испытаний над разными числами.

Докажите это свойство.

Не менее любопытные закономерности можно обнаружить, подсчитывая сумму кубов или сумму четвертых

степеней цифр любого числа и повторяя эту операцию над получающимися суммами.  Впрочем, оставлю эти

наблюдения и выводы из них как тему для ваших самостоятельных изысканий.