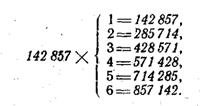1. Вынимаю из бездонной числовой шкатулки число 142 857. Оно состоит из шести разных цифр. Расположим
|
|
|
|
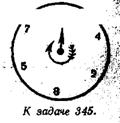
их по кругу в виде циферблата (см. рисунок). Умножим теперь данное число последовательно на 1, 2, 3, 4, 5 и 6:
Перемещаясь по циферблату вместе со стрелкой, мы прочтем любое из получившихся произведений.
Каждое число циферблата служит первой цифрой ;
одного из результатов произведения. Настоящая числовая карусель, не правда ли? ‘
2. Есть еще одно интересное свойство. Если любое из этих произведений рассечь на две грани по 3 цифры, а затем обе грани сложить, то во всех случаях результатом будет одно и то же число: 999. В самом деле, 142+ 857=999, 285 + 714 =999 и т. д.
3. Продолжим наши наблюдения над произведением числа 142 857 на целые числа, следующие за числом 7 (произведение на 7 рассмотрим позже):
Получаются семизначные числа, но тоже особенные: если зачеркнуть первую цифру и ее же прибавить к последней (см. равенства в круглых скобках), снова получим одну из круговых перестановок числа
Та же «карусель» из цифр числа 142 857 (за немногими исключениями) будет получаться и далее с восьмизначными результатами произведения, если только зачеркивать первые две цифры и прибавлять их к последним двум.
4. Произведение числа 142 857 на 7 резко отличается от остальных произведений. Оно состоит из одних девяток:
Вот это обстоятельство и проливает свет как на происхождение самого числа 142 857, так и на его «таинственные» свойства. Не будет ли оно периодом дроби 1/7 при
обращении ее в десятичную? Делим 1 на 7:
Последний остаток повторил число 1, следовательно, при дальнейшем делении в частном будут повторяться те же цифры и в том же порядке. Это и есть периодическая дробь, то есть такая бесконечная дробь, в последовательности десятичных знаков которой обнаруживаются (начиная с некоторой цифры) повторения группы цифр.
Предположение оправдалось: число 142 857 действительно является периодом дроби 1/7 при обращении ее в десятичную. Чтобы уяснить, почему это число при умножении на 2, 3, 4, 5 и 6 дает лишь круговую перестановку своих цифр, вернемся к действию деления 1 на 7. Весь процесс обращения дроби 1/7 в десятичную можно расчленить на следующие этапы:
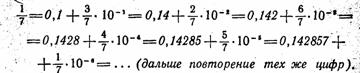
Отсюда ясно, что при обращении дроби
в десятичную период начнется с цифры, расположенной после цифры 1 в числе 1 428 571 428 5714 … , то есть периодом будет 428 571; это же число, очевидно, должно быть и произведением числа
так как
Далее, при обращении дроби
в десятичную период начнется с цифры, расположенной после цифр 1 и 4 в числе 14 285 714 285 714 … , то есть периодом будет
285 714; это же число, очевидно, должно быть и произведением 142 857 на 2, так как
i т. д.
Taкже нетрудно уяснить, почему произведение числа, 142 857 на 7 состоит из одних девяток. Дело в том, что десятичная дробь с бесконечно повторяющимися девятками после запятой считается равной 1, то есть
и произведение дроби 1/7 на 7 тоже равно 1.
. 5. Если дробь
обращается в периодическую, то период ее может иметь не больше чем
цифр. В самом деле, при делении остаток всегда должен быть меньше делителя, но существует только конечное число целых чисел, меньших b, а именно 1, 2, 3, … b – 1.
Каждое из этих чисел может быть остатком при делении a на b , и каждому из них соответствует какая-либо цифра частного, Дальше возможно только повторение остатков, а значит, и повторение цифр частного. Отсюда и следует, что наибольшее возможное число цифр в периоде на 1 меньше знаменателя.
В дроби 1/7 достигнута именно эта максимальная длина периода (6 цифр).
Период называется полным, если он состоит из наибольшего возможного при данном знаменателе числа цифр.
Но не всякая дробь имеет полный период. Например, период дроби 1/39 содержит не 38 цифр, а только 6:
1/39=0,025641025641…
«Круговое» свойство числа 142 857, являющегося полным периодом дроби 1/7, присуще также периоду любой другой периодической дроби, если только ее период полный.
Периоды дробей 1/17 и 1/29 полные:
В первом —16 цифр, во втором — 28. Числа, образованные цифрами этих периодов, следовательно, обладают теми же свойствами, что и число 142 857.
