К той же семье «круговых» чисел, что и число 142 857, принадлежит число М = 052 631 578 947 368 421.

При помощи диска, изображенного на рисунке, оно может быть мгновенно умножено на любое целое число в пределах от 1 до 18.

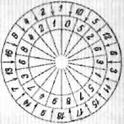
По внешнему кольцу диска, изображенного на рисунке, размещены все восемнадцать множителей. По внутреннему кольцу — все цифры множимого М; эти же цифры образуют и каждое из восемнадцати произведений.

Чтобы прочитать результат умножения числа М на любое из чисел внешнего кольца, надо полностью обойти внутреннее кольцо, начиная с цифры, указанной ближайшей стрелкой, находящейся справа от множителя, если смотреть на цифры из центра диска. Двигаться при этом следует по ходу часовой стрелки.

Например, ближайшая стрелка справа от числа 14, расположенного на внешнем кольце, указывает на цифру 7. Это значит, что число 736 842 105 263 157 894 есть результат умножения числа М на 14. Проделайте еще несколько умножений числа М. Произведение числа М на 19 уже совсем иное; оно состоит из одних девяток, и вы немедленно догадываетесь, что число М представляет собой период дроби 1/19 при ее обращении в десятичную. Период этой дроби оказался «полным» (содержит 18 цифр), следовательно, он обладает свойством цикличности (повторяемости одних и тех же цифр), описанным в задаче 345, чем и объясняется «секрет» нашего диска.

Приготовьте из картона несколько разных дисков мгновенного умножения из периодов других дробей и демонстрируйте друзьям свою феноменальную способность быстрого счета. Для этого пригодны дроби только с полными периодами, например, рассмотренные выше дроби 1/7, 1/17, 1/19, 1/29.

А еще какие дроби имеют полный период? В поисках таких дробей вы легко подметите, кстати, что период всякой дроби с простым знаменателем (о простых числах см. стр. 358) либо полный, либо число цифр у него равно одному из делителей возможного полного периода.