I. Чтобы написать все числа от 1 до 26, достаточно, конечно, иметь в своем распоряжении все 10 цифр: 0, 1, 2,…, 9. Достаточно, но не необходимо. При желании можно обойтись всего лишь одной цифрой 2, употребляя ее при этом ровно по пять раз для записи каждого числа и пользуясь только четырьмя арифметическими действиями, включая возведение в квадрат, и скобками. Займитесь на досуге этой умственной гимнастикой.
Вот для примера первый десяток чисел:
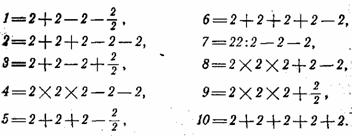
По приведенному образцу представьте и каждое из последующих 16 чисел (от 11 до 26 включительно).
Изобразить число 27 пятью двойками при таких условиях не удается.
Еще раз напоминаю, что для изображения каждого числа должно быть употреблено ровно пять двоек.
II. При помощи цифры 4, если условиться употреблять ее непременно четыре раза, изобразите все целые
числа в пределах от 1 до 10.
III. Для любителей числовых головоломок обобщим предыдущую задачу.
Изобразить целое число при помощи ровно четырех любых одинаковых цифр, соединяя их математическими
знаками. Это значит изобразить число четырьмя цифрами так, чтобы при замене этих цифр четверкой любых
других одинаковых цифр (кроме нуля) получилось то же число. Возьмем, например, изображение числа 3 четырьмя четверками: 3=(4+4+4) : 4.
При этом способе изображения числа 3 цифра 4 заменима любой другой цифрой (кроме нуля). Например, 3=(5+5+5) : 5, или 3=(8+8+8) :8
и вообще
3 = (n + n + n):n.
Но в изображении числа 5 при помощи четырех четверок 5=(4х4+4) : 4, цифру 4 нельзя заменить никакой другой цифрой. Надо искать, следовательно, другой способ изображения числа 5. При этом разрешается употреблять знаки сложения, вычитания, умножения и деления, скобки. Если этих знаков окажется недостаточно, то еще
1) знак квадратного радикала
(имея в виду арифметическое значение корня, то есть только его положительное значение из положительного числа:
но не —3);
2) знак факториала !; этот знак ставится справа от числа и обозначает произведение всех натуральных чисел
от 1 до этого числа включительно, например
вообще
3)точку перед числом (на уровне строки), например, .4; точку перед числом и над числом, например, .4. Первым символом принято в некоторых странах обозначать десятичную дробь: .4=0,4, а вторым — периодическую: .4 = =0,(4). Напомню, что периодическая дробь точно заменяется простой дробью:
Подумайте над тем, как, пользуясь указанными математическими знаками, изобразить целое число при помощи любых четырех одинаковых цифр.
Примеры.
где n – любая цифра от 1 до 9.
Пусть в последнем примере, скажем, n=7, тогда
Сами додумайтесь до изображения всех целых чисел в промежутке от 1 до 21 при помощи только четырех n, где n можно было бы заменить любой цифрой, кроме нуля. Из указанного промежутка чисел не удается изобразить только число 14. Если придумаете — сообщите.
Предупреждение. «Решение», подобное
не годится, так как это равенство справедливо только при n=8, а по условию n должно быть любой цифрой.
IV. Если одна цифра 2, употребленная не более 5 раз, или одна цифра 4, употребленная не более 4 раза в состоянии заменить собой любую из цифр от 1 до 9, то и вся эта дружная семья цифр не остается в долгу.
Участвуя всей семьей сразу (но без нуля), они могут заменить собой любую цифру своего же семейства.
Вот как, например, они заменяют 2 и 4:
|
|
Каждая из этих неправильных дробей содержит все цифры от 1 до 9, причем каждую только по одному разу.
Составляя аналогичные дроби из тех же цифр и употребляя каждую цифру только по одному разу, вы можете образовать числа 3, 5, 6, 7, 8 и 9, то есть все остальные однозначные числа, кроме 1.
Для изображения 1 посредством девяти цифр надо придумать особый способ.
Не торопитесь обращаться к ответу, сначала попытайтесь найти его самостоятельно.
V. Вернем изгнанника (нуль) в семейство остальных цифр. Теперь при помощи десяти различных цифр можно составить шесть таких дробей, что каждая из них будет равна 9. Три дроби таковы:
А остальные три составьте сами. Единицу, конечно, тоже очень легко образовать из десяти цифр (составьте!). Можно попытаться составить и другие однозначные числа из всех десяти цифр.
