Бесконечно много разнообразных соотношений между числами. Одни из них значительны и являются предметом серьезных исследований. Другие менее существенны; их свойства узки, единичны, но именно своей исключительностью они иногда и привлекательны. Назовем их «числовыми находками».
I. Среди целых чисел обнаружено несколько пар таких, что сумма и произведение чисел каждой пары отличаются только расположением цифр:
II. Несколько пар двузначных чисел замечательны совсем другим свойством: произведение, составленное из пары чисел, не изменится, если в каждом из сомножителей переставить цифры. Взгляните:
Есть еще 4 пары двузначных чисел, обладающих этим свойством. Найдите их.
III. А вот еще три пары последовательных чисел, квадраты которых пишутся теми же цифрами, но в измененном порядке:
IV. Нет ли среди целых чисел хотя бы одного, которое обладало бы следующими свойствами:
1) оно должно быть четвертой степенью суммы его же цифр (отсюда следует, что оно должно быть и точным квадратом некоторого числа);
2) если разбить его на три грани по 2 цифры, то сумма трех полученных двузначных чисел тоже должна быть точным квадратом;
3) если написать его в обратном порядке цифр и снова разбить на 3 грани по 2 цифры, то сумма и этих трех двузначных чисел должна быть точным квадратом.
В результате произведенных вычислений такое число было обнаружено. Вот оно:
234 256.
Оно обладает всеми требуемыми свойствами. Убедитесь! I
V. Числа, подобно звездам, мы группируем в разнообразные числовые «созвездия».
«Созвездие» из шести чисел 2, 3,7, 1, 5,6 занятно тем, что сумма первых трех чисел равна сумме последних трех, но равны даже и суммы их квадратов:
Можно сказать, что эти числа 2, 3,7, 1, 5 и 6 заменяют собой шесть неизвестных
в системе уравнений
Есть бесконечно много, и других чисел, которые удовлетворяют этой системе уравнений. Интересно, как быстро удалось бы вам подобрать еще хотя бы одну группу из шести подходящих чисел?
Еще ярче «созвездия» из восьми чисел
0, 5, 5, 10, 1, 2, 8, 9
и из десяти чисел
1, 4, 12, 13, 20, 2, 3, 10, 16, 19.
В каждом из них сумма чисел первой половины равна сумме чисел второй половины, затем, как и в предыдущем
примере, равны суммы квадратов тех же чисел; больше того, равны даже суммы кубов тех же чисел:
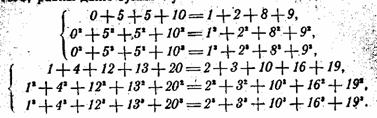
Несомненно, имеются и другие группы чисел, связанных точно такими же соотношениями, но как подобрать
такие числа?
В «тайну» всех приведенных здесь «числовых созвездий» первыми проникли еще 200 лет назад (в 1750—1751 гг.) два петербургских академика: Гольдбах и гениальный Эйлер. Они нашли ряд формул, пригодных для решения в целых числах некоторых систем уравнений, в частности и тех, которые приводят к упомянутым «числовым созвездиям».
Так, для подбора чисел, образующих первое «со-
звездие»:
оказались пригодными такие формулы:
и
Надо только заменить в этих формулах буквы а, Ь и с любыми числами, и вы получите столько чисел этого «созвездия», сколько захотите.
В частности, при
получается «созвездие», приведенное в качестве первого примера: 2, 3, 7, 1, 5, 6.
Составьте другие группы чисел первого «созвездия», придавая буквам а, Ь и с разнообразные значения.
Эйлер и Гольдбах дали еще и другую группу формул для чисел первого «созвездия»
где
— тоже произвольные числа.
Для подбора чисел, образующих второе «созвездие»:
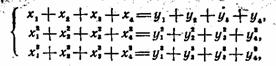
пригодны следующие формулы:
Опять заменяйте буквы а и Ь любыми числами, и вы получите столько чисел второго «созвездия», сколько захотите.
Полезно проверить приведенные здесь формулы не только на частных примерах, но и в общем виде, заменяя в каждом уравнении все неизвестные их значениями.
VI. Много числовых находок связано с решением уравнений в целых числах. Труд, настойчивость и математическая смекалка все время пополняют наш сундучок с «числовыми созвездиями» новыми любопытными образцами.
Не хотите ли ознакомиться, например, с одним из новых, очень пышных «созвездий». Суммы всех степеней, от первой до пятой, шести чисел: 1, 6, 7, 17, 18 и 23, равны суммам тех же степеней других шести чисел: 2, 3, 11, 13, 21 и 22:
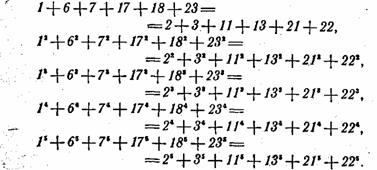
«Ключом» к получению других чисел этого «созвездия» служит тождество:
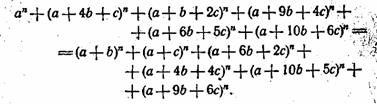
Замените буквы а, Ь и с любыми числами, а букве n придайте значения сначала 1, затем 2, 3, 4 и 5, и вы получите столько раз по 5 равных сумм, сколько захотите.
VII. Вы еще можете сформировать красивые суммы квадратов двузначных чисел с переставленными цифрами. Для этого сначала составьте две группы с одинаковым количеством таких однозначных чисел, чтобы сумма квадратов чисел первой группы равнялась сумме квадратов чисел второй группы, например
А теперь из чисел 4, 5, 6 и 8, 3, 2 составьте три двузначных числа, используя первые три числа как десятки, а последние три как единицы, объединяя их произвольным образом. У вас образуются непременно такие три двузначных числа, что сумма их квадратов будет равна сумме квадратов обращенных чисел.
Так, из групп чисел 4, 5, 6 и 8, 3, 2 можно образовать следующие равенства:
или
В этих равенствах все числа правой стороны являются обращенными числами левой стороны.
Обратите внимание еще на такую красивую черту этих равенств: цифры в каждом из них расположены симметрично относительно знака равенства.
Обобщая, можно сказать, что если n однозначных чисел
и n других однозначных чисел
связаны равенством
то непременно будет справедливо и такое равенство:
Кто пожелает, может убедиться в этом, раскрывая скобки во втором равенстве и принимая во внимание первое равенство. Поупражняйтесь в составлении таких сумм. Возьмите, например, восемь первых чисел натурального ряда: 1, 2, 3, 4, 5, 6, 7 и 8. Сообразите, которые из них должны быть числами группы
а которые — числами группы
а затем, следуя указанному правилу, составьте несколько равных сумм квадратов двузначных чисел с переставленными цифрами.
VIII. Новинкой же нашего сундучка с «числовыми созвездиями» являются и еще более замысловатые группы двузначных чисел с переставленными цифрами. Например,
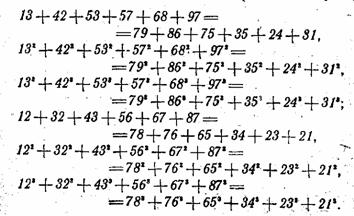
Исследуйте, нет ли и здесь связи между суммами степеней однозначных чисел и искомыми суммами.
IX. Еще одна находка! Число 145 уникально; только оно может быть выражено суммой факториалов (о факториале см. в задаче 349, III) своих цифр (если не считать тривиальных случаев 1 = 1! и 2=2!):
Будем считать, что 0! = 1 , тогда указанным свойством обладает еще только одно число: 40 585. Действительно,
Это число и доказательство единственности чисел 145 и 40 585 нашел (одним из первых) студент Н. Н. Головин
(Ташкент).
Кто захочет самостоятельно продумать доказательство, тот, вероятно, натолкнется и на такие числа, каждое из которых только на +1 или на —1 отличается от суммы факториалов его цифр. Какие это числа и сколько их всего?
X. Есть только два трехзначных числа, любая целая и положительная степень которых оканчивается теми же тремя цифрами и в том же порядке:
Как нашли эти трехзначные числа и как установили, что их только два? Это была одна из задач ежегодного конкурса, проводимого журналом Математика в школе для всех любителей математической смекалки. Она имеет короткое, но довольно замысловатое решение. Разобраться в нем, конечно, полезно, но еще полезнее приложить собственные усилия к отысканию решения.
Докажите самостоятельно, что если вторая степень какого-либо n-значного числа оканчивается цифрами, изображающими его первую степень, то и всякая другая целая положительная степень этого числа оканчивается
теми же цифрами.
Например,
оканчивается на 76, тогда этими же цифрами будет оканчиваться и 76m , где m — любое целое положительное число.
