I. Расположим натуральные числа 1, 2, 3, 4, … в форме треугольника:

Вглядитесь в этот числовой треугольник, и вы, несомненно, обнаружите немало закономерностей в расположении чисел по строкам и столбцам, связей между числами и местами, занимаемыми ими, и т. п. Заметили ли вы, например, что
1) нижнее число каждого столбца — квадрат номера столбца;
2) произведение любых двух соседних чисел какой-либо строки есть число той же строки; например, 5×11=55; оба сомножителя и произведение вы найдете в одной строке; место в строке, занятое таким произведением, определяется как сумма числа 1 и меньшего множителя; отсчет надо вести слева направо, начиная с того места, которое занимает меньший множитель; например, произведение 5×11=55 расположено в той же строке, где 5 и 11, на 1+5=6 месте, начиная с числа 5; 7×13=91 расположено в соответствующей строке на 1+7=8 месте, начиная с числа 7;
3) все числа строки, отмеченной звездочкой (*), получаются по формуле
![]()
в этой строке после числа 3 каждое третье число делится на 3; каждое седьмое число после числа 7 или 21 делится на 7; каждое тринадцатое число после 13 или 91 делится на 13 и т. д.; аналогичными свойствами обладают числа каждой строки.
II. Нельзя ли всю последовательность натуральных чисел
![]() в порядке их следования разбить на пары равных сумм?
в порядке их следования разбить на пары равных сумм?
Попробуем. Первая пара сразу бросается в глаза: 1+2=3. Испытаем следующие числа: 4+5+6=7+8.
Пока удается. Еще несколько попыток, и опять успех:
9+10+11+12=13+14+15.
Замечаем, что количество слагаемых нарастает, но нарастает закономерно: каждый раз как в левой части равенства, так и в правой прибавляется по одному слагаемому, причем в левой части каждого равенства слагаемых на одно больше, чем в правой. Проверим это на следующей паре сумм:
16+17+18+19+20=21+22+23+24.
Подтверждается!
Посмотрим теперь, что представляет собой наименьшее слагаемое (крайнее слева) каждой пары равных сумм. Наблюдения показывают, что оно есть квадрат числа слагаемых той суммы, в которой слагаемых меньше.
В самом деле, правая часть первого равенства состоит из одного числа (3) и наименьшее слагаемое в этом равенстве 12; в правой части второго равенства — два слагаемых (7+8) и наименьшее слагаемое в этом равенстве
![]() в правой части третьего равенства — три слагаемых и наименьшее слагаемое в этом равенстве З2, и т. д.
в правой части третьего равенства — три слагаемых и наименьшее слагаемое в этом равенстве З2, и т. д.
Последняя закономерность позволяет быстро написать пару равных сумм, соответствующих заранее намеченному числу слагаемых.
Пусть, например, требуется найти 7 последовательных чисел, удовлетворяющих условию. Определяем наименьшее слагаемое: сначала находим, что 7—1=6; это число определяет количество слагаемых в правой части равенства, а наименьшее слагаемое равно 62=36.
Следовательно, искомая пара равных сумм такова:
36+37+38+39+40+41+42=43+44+45+46+47+48.
Итак, наблюдения показали, что сумма n+1 последовательных чисел, в которой наименьшее слагаемое
![]() равна сумме n следующих за ними чисел. Если первое слагаемое первой суммы
равна сумме n следующих за ними чисел. Если первое слагаемое первой суммы
![]() то второе слагаемое этой суммы, по условию, на 1 больше, третье слагаемое на 2 больше, четвертое на три больше,
то второе слагаемое этой суммы, по условию, на 1 больше, третье слагаемое на 2 больше, четвертое на три больше,
![]() слагаемое на n больше, чем первое; значит, последнее слагаемое первой суммы будет
слагаемое на n больше, чем первое; значит, последнее слагаемое первой суммы будет
![]() Отсюда первое слагаемое второй суммы, по условию,
Отсюда первое слагаемое второй суммы, по условию,
![]() , второе слагаемое, как и раньше, на 1 больше, третье — на 2 больше, n-е слагаемое на n—1 больше, чем первое; значит, последнее слагаемое второй суммы
, второе слагаемое, как и раньше, на 1 больше, третье — на 2 больше, n-е слагаемое на n—1 больше, чем первое; значит, последнее слагаемое второй суммы
![]() или
или
![]() Окончательно результат наших наблюдений можно выразить в следующей алгебраической форме:
Окончательно результат наших наблюдений можно выразить в следующей алгебраической форме:
|
|
Знакомые с формулой суммы чисел, составляющих арифметическую прогрессию, без больших усилий докажут справедливость этого равенства.
III. После успешных наблюдений над суммами натуральных чисел обратимся к суммам квадратов натуральных чисел.
Рассмотрим прежде всего сумму квадратов n последовательных натуральных чисел:
![]()
Это — не прогрессия. Для определения этой суммы нужна специальная формула, и она приводится в учебниках алгебры:
![]()
Если складываются квадраты только четных или, наоборот, только нечетных чисел натурального ряда, то нужны другие формулы. Сумму квадратов всех нечетных чисел от 1 до 9 можно, например, вычислить по такой
формуле:
|
|
В применении же к сумме квадратов всех четных чисел от 2 до 10 удобен такой вид формулы:
![]()
Складывая эти два равенства, получим такую разновидность формулы для суммы квадратов всех целых чисел от 1 до 10:
![]()
Сами распространите эти формулы на любое количество слагаемых.
IV, Если катеты треугольника 3 и 4, а гипотенуза 5 (так называемый египетский треугольник), то
![]()
Здесь сумма квадратов двух последовательных натуральных чисел равна квадрату следующего числа.
Еще одно наблюдение. В конце XIX века живописец-жанрист Н. П. Богданов-Вельский (1868—1945) написал картину Трудная задача, на которой изобразил группу учеников сельской школы, задумавшихся над решением «в уме» задачи С. А. Рачинского, записанной учителем на школьной доске:
![]()
Действительно, нелегкая задача для быстрого решения «в уме», если не знать «секрета». А «секрет» очень прост. Дело в том, что
![]() Следовательно, искомый ответ 2.
Следовательно, искомый ответ 2.
Но обратим внимание на другое. Из сопоставления выше написанных равенств следует, что
![]() то есть сумма квадратов нескольких последовательных натуральных чисел равна сумме квадратов следующих чисел, и опять (как в этой же задаче п. II) число слагаемых в левой части равенства только на одно больше, чем в правой. Я предвижу по крайней мере два вопроса с вашей стороны:
то есть сумма квадратов нескольких последовательных натуральных чисел равна сумме квадратов следующих чисел, и опять (как в этой же задаче п. II) число слагаемых в левой части равенства только на одно больше, чем в правой. Я предвижу по крайней мере два вопроса с вашей стороны:
1. Имеются ли, кроме чисел 3 и 4, другие два последовательных числа, сумма квадратов которых была бы равна квадрату следующего за ними числа, а кроме чисел 10, 11, 12,— другие три последовательных числа,
сумма квадратов которых была бы равна сумме квадрат двух непосредственно за ними следующих чисел?
2. Можно ли образовать равные суммы квадратов последовательных натуральных чисел, состоящие из четырех и трех слагаемых, из пяти и четырех слагаемых вообще из n+1 и n возрастающих слагаемых?
Ответ на эти вопросы содержится в решении такой вполне доступной задачи:
найти n+1 последовательных чисел, сумма квадратов которых равна сумме квадратов следующих л чисел.
V. Среди натуральных чисел нет даже двух последовательных кубов, сумма которых равнялась бы кубу следующего числа. Убедиться в этом поможет алгебра.
Если любые три последовательных числа обозначить как
![]() то, по условию,
то, по условию,
![]()
или, после преобразований:
![]()
Придадим получившемуся кубическому уравнению такой вид:
х2 (х — 6) = 2.
Легко обнаружить, что этому уравнению не удовлетворит ни одно целое число. В самом деле, правая часть уравнения — число положительное, следовательно, х должен быть больше шести. Самое меньшее возможное значение для х — это семь. Но при х=7 левая часть уравнения значительно превысит правую и будет превышаь ее при всех последующих значениях х, то есть убеждаемся что действительно среди целых чисел нет корней получившегося кубического уравнения.
Однако любителям подобного рода числовых головоломок удалось и из кубов последовательных чисел закономерно составить равные суммы, правда, всякий раз с некоторыми добавлениями:

В квадратных скобках — суммы кубов последовательных чисел, причем опять на каждые n слагаемых в правой скобке приходится n + 1 слагаемых в левой скобке; в круглых скобках как справа, так и слева — одинаковые суммы кубов последовательных чисел, начиная с 1.
Замечено, что выделенное жирным шрифтом число (без показателя) в каждом равенстве связано с числом слагаемых в квадратных скобках следующим образом: выделенное жирным шрифтом число равно утроенному произведению числа членов слева на число членов справа (в квадратных скобках). Так, в первом равенстве в левой квадратной скобке 2 члена, а в правой 1 и, следовательно,
3(2∙1)=6.
Во втором равенстве в левой квадратной скобке 3 члена, а в правой 2 и соответственно
![]()
В третьем равенстве
![]()
Не останавливаясь на выяснении общности подмеченной закономерности, ограничимся составлением и практической проверкой равенства таких курьезных сумм еще для одного частного случая. Пожелаем, например, чтобы в левой квадратной скобке было 5 слагаемых, а в правой 4. Утроим их произведение:
![]() Тогда
Тогда
![]()
Убедитесь арифметически в справедливости этого равенства!
Между прочим, аналогичные закономерности можно подметить также и у равных сумм самих натуральных чисел и их квадратов. Вспомните, какие мы имели равенства для первых степеней:
1+2=3,
4 + 5 + 6 = 7 + 8,
9 + 10 + 11 + 12=13 + 14 + 15;
(выделенное жирным шрифтом число равно произведению числа слагаемых слева и справа от знака равенства);
для вторых степеней:
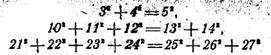
(выделенное число без показателя степени равно удвоенному произведению числа слагаемых слева на число слагаемых справа от знака равенства).
VI. Знакома ли вам такая таблица умножения:

Произведение какого-нибудь числа верхней строки на любое число крайнего слева столбца расположено на пересечении столбца и строки, занимаемых сомножителями. Так, например, число 12 расположено на пересечении четвертого столбца и третьей строки или шестого столбца и второй строки.
Но, рассматривая внимательно эту таблицу, вы найдете еще несколько любопытных соотношений:
1. Сумма чисел в любом квадрате с вершиной в левом верхнем углу таблицы есть полный квадрат (то есть представляет собой квадрат некоторого числа):

2. Каждый из вышеупомянутых квадратов образуется путем присоединения к предыдущему квадрату согнутой под прямым углом полоски, называемой гномоном. Сумма чисел в любом гномоне представляет собой куб некоторого числа:

3. Каждый из вышеупомянутых квадратов состоит из 1, 2, 3, …. n гномонов. Отсюда следует формула,
известная еще с античных времен:
![]()
Так как
![]() (сумма членов арифметической прогрессии), то
(сумма членов арифметической прогрессии), то
![]()
Можно предложить, пожалуй, несколько неожиданную геометрическую интерпретацию этой формулы и отдельных чисел, входящих в состав гномонов.
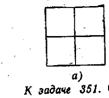

Подсчитайте-ка число всех прямоугольников на рисунках а и б (включая и квадраты). На рисунке а их 9:

Как видно, левый столбец состоит из чисел, входящих в состав гномонов, образующих квадрат (см. таблицу на стр. 348). Значит, в квадрате, состоящем из 22 равных клеток, содержится 13
+ 23 = 9 прямоугольников; в квадрате, состоящем из 32
равных клеток, содержится 13 +23+33=36 прямоугольников. А если так, то сколь же всего прямоугольников в квадрате, состоящем из n2
равных клеток?
VII. В классической формуле для суммы кубов слагаемыми являются по порядку идущие числа натурального ряда: 1, 2, 3, 4 и т. д. Математик Лиувилль (Франция) поставил более широкую задачу найти произвольные целые числа a, b, c, d, …, сумма кубов которых равнялась бы квадрату их суммы:
a2
+ b2 + c2 + … = (a + b +c + … )2.
Среди чисел a, b, c, d,… допускаются и равные между собой.
Подобрать подходящие числа, не руководствуясь при этом каким-нибудь правилом, просто наудачу — дело почти безнадежное.
Сделайте все-таки две-три попытки, а потом продолжайте чтение.
Лиувиллю удалось получить занятный результат, суть которого легко уяснить на следующих двух примерах.
Пример 1. Возьмем число 6. Оно делится на 1, 2, 3 и 6. А сколько же делителей у каждого из этих делителей? У числа 1 — один делитель, у числа 2 — два делителя (1 и 2), у числа 3 — два делителя (1 и 3) и, наконец, у числа 6 — четыре делителя (1, 2, 3 и 6). Вот эти числа делителей 1, 2, 2 и 4 и удовлетворяют интересующему нас соотношению, то есть имеем:
13+23 + 23 +43
= (1+2+2+4)2=81.
Пример 2. Возьмем число 30. Его делители: 1, 2, 3, 5, 6, 10, 15, 30. Число делителей у каждого из них соответственно 1, 2, 2, 2, 4, 4, 4, 8. Имеем:
13+23 + 23 + 23 +43
+43 +43 +83 = (1+2+2+2+4+4+4+8)2.
Способ простой и остроумный. Примените его самостоятельно к другим числам.
VIII. Наблюдения над рядом натуральных чисел можно, разумеется, вести бесконечно. Вот еще один пример любопытного соотношения между натуральными числами.
Разделим ряд натуральных чисел на следующие группы: 1; 2, 3; 4, 5, 6; 7, 8, 9, 10; … В первой группе — одно число, во второй—два следующих, в третьей — три и т. д., в n-й группе — n чисел. Замечаем, что первое и последнее числа в каждой группе определяются по формулам:
((n – 1)n)/2 + 1 и (n(n +1))/2,
где n— номер группы.
Числа каждой группы составляют арифметическую прогрессию с разностьюd = 1. Зная число членов (n) в каждой группе, а также ее первый (a1) и последний (an) члены, можно подсчитать сумму чисел в каждой группе.
Сумма членов арифметической прогрессии определяется по формуле:
S = ((a1 + an)n)/2
Для каждой группы:
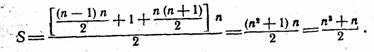
Обозначив суммы различных групп через S1, S2, S3, S4, … и интересуясь только суммами групп с нечетными номерами, будем иметь:

Сумма всех этих сумм равна

Для любителей алгебраических преобразований здесь возникает увлекательная задача.
Задача. Доказать, что
![]()
Указание. Предварительно преобразуйте формулу для суммы кубов (см стр. 349) так, чтобы получилась формула для суммы кубов нечетных чисел:
![]()
Вернемся к сумме
![]() В результате преобразований, которые только что предлагались ваш для выполнения, мы имеем
В результате преобразований, которые только что предлагались ваш для выполнения, мы имеем
![]()
Эта формула раскрывает нам довольно любопытное соотношение между указанными группами чисел:
1; 2, 3; 4, 5, 6; 7, 8, 9, 10; …,
а именно: если из ряда этих групп выкинуть группы с четными номерами (вторую, четвертую и т. д.), а оставшиеся группы сложить, то их сумма будет равна четвертой степени числа складываемых групп.
Так, например, сразу можно сказать, что сумма 1 + (4+5+6)+(11+12+13+14+15) равна З4, то есть 81.
IX. Всякий, кто заинтересовался рассмотренными зависимостями, связывающими натуральные числа, не мог не заметить простейших свойств их сумм, в частности сумм нечетных чисел: 1, 3, 5, … (2n — 1).
Сумма первых двух нечетных чисел 1 + 3 равна 22, квадрату числа 2.
Сумма первых трех нечетных чисел 1+3+5 равна З2, квадрату числа 3.
Сумма первых четырех нечетных чисел 1+3+5+7 равна 42, квадрату числа 4 и т. д.
Это свойство сумм нечетных чисел становится весьма наглядным, если представить себе квадрат (см. рисунок а на стр. 353), разделенный на согнутые под прямым углом полоски (гномоны), каждый из которых состоит из единичных квадратов и является иллюстрацией нечетного числа. Последовательное присоединение гномонов к первому единичному квадрату не нарушает формы квадрата (см. рисунок б) и тем самым иллюстрирует
свойство суммы нечетных чисел образовывать квадратное число.
Естественно предположить, что подмеченная закономерность сохраняется для суммы любого количества n

первых нечетных чисел, то есть что эта сумма всегда равна квадрату числа слагаемых:
![]()
А вдруг это предположение не подтвердится? Не перестанут ли наши суммы подчиняться найденному закону, начиная с какого-нибудь, может быть очень большого, числа слагаемых?
С закономерностями, обнаруженными опытным путем, вполне может так случиться.
Так как ряд натуральных чисел бесконечен, то опытным путем невозможно проверить подмеченную закономерность для сумм нечетных чисел. Но в этом и нет необходимости. Математика имеет средства предвидеть результат.
Рассуждаем так: пусть для какого-нибудь числа к слагаемых справедливо утверждение, что их сумма равна квадрату их числа:
![]()
Прибавим теперь следующее нечетное число:
![]() и посмотрим, сохранится ли та же закономерность для
и посмотрим, сохранится ли та же закономерность для
суммы
![]() слагаемых:
слагаемых:

Закономерность сохранилась!
Сумма по-прежнему равна квадрату числа слагаемых. Так мы установили, что если предполагаемая закономерность имеет место хотя бы для одного какого-нибудь числа к слагаемых, то она остается справедливой и для числа слагаемых, на единицу большего чем k.
Значит, опытную проверку закономерности надо произвести, но только один раз. Возьмем самое меньшее число слагаемых: два. Имеем: 1+3=22. Сумма двух слагаемых (k=2) равна квадрату числа слагаемых. Следовательно, по доказанному, закономерность сохранится и для трех членов (k + 1=3); но если она верна для трех слагаемых (k=3), то она сохранится и для четырех (k+1 =4); если она верна для k=4, то она сохранится и для k+1=5; если она верна для k=5, то она сохранится и для k+1=6 и т. д.
Этот простой, но строгий способ рассуждений называется математической индукцией.
Итак, сомнения рассеяны! Сумма n первых нечетных чисел при любом числе n слагаемых равна квадрату числа слагаемых. В справедливости формулы
![]()
для любого n можно было бы убедиться простым подсчетом суммы
1+3 + 5+…+(2n-1)
по формуле для суммы членов арифметической прогрессии (сделайте!), но по сути дела это был бы тот же способ рассуждений, так как применимость формулы для суммы членов арифметической прогрессии тоже опирается на принцип математической индукции.
X. Не менее любопытна и еще одна особенность сумм нечетных чисел. Если ряд нечетных чисел, начиная с 1, разделить на группы, отделив для первой группы одно число, для второй—два, для третьей—три, и т. д.,
то сумма чисел каждой группы будет равна кубу номера Группы (теорема Никомаха):

Каждая строка — сумма n членов (n — номер строки) арифметической прогрессии с постоянной разностью d=2, по первый и последний члены этой прогрессии разные в разных строках. Зависят ли они от номера строки? Несомненно.
Если хотите доказать справедливость высказанного свойства для любого n, то сначала мобилизуйте свою смекалку на отыскание зависимости между первым членом арифметической прогрессии и номером (n) строки, которую составляет сумма этой прогрессии.
Если через an
обозначить первый член строки, номер которой
![]() и т. д. Так вот прежде всего и докажите, что
и т. д. Так вот прежде всего и докажите, что
![]()
Но имейте в виду: на одной догадке далеко не уедешь. Ищите путь решения.

