Несколько предварительных замечаний.

1.            Многочленом называется алгебраическое выражение вида:

где n — число целое, положительное; коэффициенты а₀, а₁, . . ., а_n — любые действительные числа; под буквой х также подразумевается любое действительное число.

2.            Если один многочлен (р) указанного вида равен произведению двух других (m₁, и m₂), р=m₁m₂, то мы говорим, что многочлен р делится на многочлен m₁ (или m₂) и в частном получается многочлен m₂
(или m₁).

Например, х²—9 делится на Зх+9 и в частном получается

Действительно,

Заметим, между прочим, что часть коэффициентов частного — дробные числа, в то время как все коэффициенты делимого и делителя — целые.

3.            Из факта делимости одного многочлена с целыми коэффициентами на другой многочлен также с целыми коэффициентами еще не следует, что делятся числа, в которые обращаются делимое и делитель при замене х любым целым числом, если, разумеется, делимость рассматривать с точки зрения арифметики целых чисел.

Например, как мы видели выше,

При х=6 делимое обращается в число 6²—9=27, делитель— в число 3∙6+9=27, и здесь делимое делится на делитель: 27 : 27=1. Но при х=7 делимое обращается в число 49—9=40, делитель — в число 3∙7+9=30, и теперь делимое не делится на делитель с точки зрения арифметики целых чисел.

4.            Если же все коэффициенты многочленов—делимого, делителя и частного — целые числа, то число, в которое обращается многочлен-делимое, непременно делится на число, в которое обращается многочлен-делитель при замене х любым целым числом, кроме тех, которые обращают делитель в нуль.

Например,

(2х³ — Зх² –8х+ 12):{х² — 4) = 2х — 3.

Все коэффициенты целые, следовательно, будут делиться и числовые значения делимого и делителя при замене х любым целым числом, кроме х = ±2, так как при этих значениях делитель обращается в нуль и деление невозможно. Так, при х=3 имеем:

значение делимого: 2∙3³ — З∙З² — 8∙3 + 12= 15, значение делителя: З²— 4 = 5.

Убеждаемся в том, что первое значение делится на второе:

15 :5 = 3. Тому же числу 3 равно и значение частного: 2∙3—3 = 3.

Для решения некоторых задач, в частности для доказательства признаков делимости чисел, полезно знать, при каких условиях сумма и разность степеней двух чисел (x^m +a^m  и x^m –a^m
, m– целое положительное число) делятся на сумму и разность их оснований (х+а и х—а).

Ответ на этот вопрос дается в школьном курсе алгебры (обычно в 10-м классе). Но и для читателя, еще не добравшегося в своем образовании до 10-го класса, не составит большого труда разобраться в решении поставленного вопроса.

Алгебраические выражения х^т+ а^ти х^т—а^т—это частные виды многочлена

а_тх^m+а_т–1х^т–1+…+а₁х+а₀(*)

(под всеми буквами многочлена будем здесь подразуме­вать только целые числа, включая нуль). Если, например,

т = 4, а_т
= 1,

a_m–1=a_m–2=…=a₁=0, a₀=16,

то получается такой частный вид многочлена:   x⁴= 16, или х⁴
+ 2⁴

Не делится х ⁴+ 2⁴
на х + 2. Замечаем, что остаток не содержит х, а представляет собой некоторое число.

Легко понять, что не только в этом примере, но и во всех случаях деления многочлена на двучлен вида х + а, то есть на двучлен, содержащий х не выше чем в первой степени, остатком будет некоторое число (либо совсем не будет остатка).

Чтобы деление совершилось без остатка, надо делимое уменьшить на величину остатка. Поэтому всегда справедливо такое утверждение: делимое минус остаток равно произведению делителя и частного. Например,

(х⁴ +16) — 32=(х + 2)∙(х³ — 2х² +4х — 8).

Убедитесь непосредственной проверкой в том, что это равенство алгебраических выражений обращается в равенство чисел при замене буквы х каким угодно числом. Равенство, обладающее такой особенностью, называют для краткости тождеством.

Предположим теперь, что вы берете произвольный многочлен вида (*), делите его на двучлен вида х + а и составляете равенство

А= (х — а)В+С,

где буквой А для краткости записи я обозначил многочлен-делимое, буквой В — частное, а буквой С — остаток.

Спрашивается, всегда ли равенство

А= (х — а)В+С   (**)

будет тождеством? Ответ. Всегда.

Доказательство этого утверждения в общем виде громоздко, но любой пример подтвердит его справедливость.

Такого рода тождество (**) любопытно тем, что с его помощью можно, не производя деления, узнать остаток. Например, я сообщил вам следующие данные: делимое х+ 1, делитель х — 1, частное x³+ х² + х + 1Какое число С является остатком?

Решение. Составим равенство

x⁴+1=(x–1)(x³+ х² + х + 1)+C

Так как оно должно быть тождеством, то положим, например, х — 1. Тогда 1 + 1 = 0 + С. Отсюда С = 2. При любых других значениях х получается такое же значение С. Пусть еще, например, х = 2. Тогда

16+ 1 = (2– 1)(8 + 4 + 2 + 1) + С,

или 17 = 15 + С. Отсюда снова С = 2.

Значит, никакого иного остатка, как только С = 2, и быть не может. Проверьте делением.

Еще интереснее. Можно не знать не только остаток, Но и частное и все-таки определить остаток, не производя деления. Пусть, например, делимое х⁴ — 1, а делитель х + 1. Как узнать остаток, не производя деления?

Обозначим многочлен, являющийся частным, буквой В, а остаток — по-прежнему буквой С. Тогда

x⁴ — 1=(x + 1)В+С.

Зная, что для остатка С получается одно и то же его истинное значение при замене х любым числом, положим х = —1. Это значение х тем удобно, что оно не потребует от нас вычисления   значения  частного   В,  так  как  все равно при х = —1 выражение (х + 1)В обратится в нуль (за счет первого сомножителя).

Имеем:

(–1)⁴ —1=0 + С,

или 1—1=С. Отсюда С = 0. Оказалось, что остаток ранен нулю. Это значит, что х⁴— 1 делится без остатка ил х + 1. Проверьте делением!

Теперь можно решить и более общую задачу. При каких условиях двучлен хт-\-1 делится на х-\-1 (т — целое положительное)?

Решение. Пусть частное В, а остаток С. Имеем:

Положим x = —1, тогда
 Ясно, что если m четное (m=2n), то С = 2;   если же m нечетное (m = 2n + 1), то С = 0.

Следовательно, если m четное (m=2n), то
, или х²ⁿ
+ 1,. не делится на х+1, если же m нечетное (m = 2n + 1), то
, или х²ⁿ⁺¹
+ 1, делится на х+1. Частное, как нетрудно убедиться, будет состоять из убывающих степеней х с чередующимися знаками, так что имеем следующую общую формулу:

Что касается двучлена
, то на х—1 он делится при любом целом положительном m, а на x + 1 делится только при m четном (m = 2n).

Убедитесь в этом самостоятельно.

Для выяснения величины остатка (С) от деления двучлена вида
 следует в тождестве

 положить x = — а.

Применяя соответствующие рассуждения, нетрудно прийти к следующим выводам:

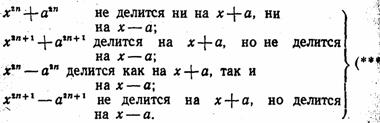
Напоминаю, что в случае делимости
 на x + a или на х — а делятся и целые числа, получающиеся в качестве делимого и делителя при замене букв а и x целыми числами (см. стр. 255).

Задача. Не вычисляя выражения 11¹⁰  – 1, доказать, что оно делится на 100.