Изложенные выше три признака делимости чисел на 7 по своему методу похожи на известные условия делимости чисел на 3 и на 9. Там и тут из цифр данного числа N при помощи простых арифметических действий
Наставляется некоторое новое число Р, от делимости которого на данный делитель зависит и делимость данного числа. Число Р составляется всякий раз так, что разность N — Р (или, может быть, сумма N + Р) делится, н данный делитель. Основой метода является делимость двучленов аn + Ьn на а + Ь при нечетном n и аn – Ьn
на а±Ь при четном n.
Применяя тот же метод рассуждений, можно убедиться в справедливости следующего любопытного признака делимости на 13, 17 и 19.
Для определения делимости данного числа на 13, 17 или 19 надо умножить крайнюю левую цифру испытуемого числа соответственно на 3, 7 или 9 и вычесть следующую цифру; результат опять умножить соответственно на 3, 7 или 9 и прибавить следующую цифру и т. д., чередуя вычитания и прибавления последующих цифр после каждого умножения. После каждого действия результат можно уменьшить или увеличить соответственно на число 13, 17, 19 или кратное ему.
Если окончательный результат делится (не делится) на 13, 17 и 19, то делится (не делится) и данное число.
Пример 1. Делится ли число 2 075 427 на 19?
Применяем правило:
2X9=18=—1
(если не желательно вводить действия с отрицательными числами, то можно оставить 18, не вычитая из него 19);
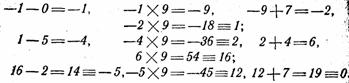
Делится.
Пример 2. Делится ли число 81 452 на 13? Применяем правило:
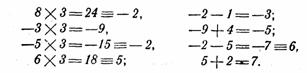
Не делится. Остаток 7.
Доказательство этого признака однотипно с изложенным выше доказательством признаков делимости на 7.
