Коробка спичек или пучок палочек одинаковой длины — отличное пособие для геометрических развлечений, требующих находчивости и развивающих сообразительность.

Из спичек можно составить всевозможные прямолинейные фигуры; превращать одну фигуру в другую путем перекладывания спичек; даже теоремы можно доказывать на спичках.

Рассмотрим для примера такую задачу:

Сколько одинаковых квадратов можно составить из 24 спичек, не ломая их и используя при этом все спички?

Если на каждую сторону квадрата употребить по 6 спичек (больше нельзя), то получится один квадрат.

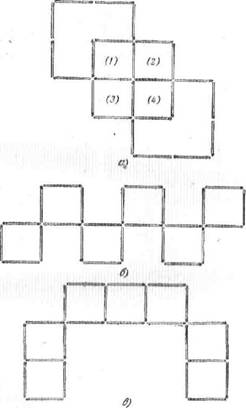
При стороне квадрата в 5 или в 4 спички одинаковых квадратов из всех 24 спичек не получится. При стороне в 3 спички можно выложить два квадрата (см. рисунок а).

При стороне квадрата в 2 спички — три квадрата (рисунок б).

Обратите внимание, что из квадратов со сторонами в 3 и 2 спички можно образовать еще дополнительные квадраты других размеров, как показано на рисунках, один дополнительный квадрат (1) из квадратов со стороной в 3 спички (рисунок ), четыре дополнительных квадрата (1) — (4) из квадратов со стороной в две спички (рис. а).

Если из каждых четырех спичек составлять один квадрат, то из 24 спичек можно образовать 6 одинаковых квадратов (рисунок б).

Если же некоторые спички дважды считать сторонами квадрата, то из 24 спичек можно образовать 7 одинаковых квадратов (рисунок в) или 8 (рисунки а и б), или даже 9 (рисунок в).

При составлении трех последних фигур образовались еще дополнительные квадраты других размеров: один на рисунке а, два на рисунке б и пять на рисунке в. Убедитесь в этом.

——

При стороне квадрата в 1/2 спички (допускаем наложение одной спички поперек другой) можно получить 16 квадратов одинакового размера и 4 дополнительных квадрата. Всего 20 квадратов (рисунок г).

Из 24 спичек при стороне квадрата в 1/3 спички может быть образовано 27 одинаковых квадратов, а с дополнительными квадратами других размеров — 42 (см. рисунок а) и, наконец, при стороне квадрата в у спички — 50 квадратов одинакового размера (см. выше рисунок б). Если же считать дополнительные квадраты (их 60), то всего получится ПО квадратов.

Сообразите, как решить следующие задачи-головоломки.

Под одним номером объединены те задачи, решение которых следует начинать с одного и того же первоначального расположения спичек. Каждая задача решается независимо от предыдущей.