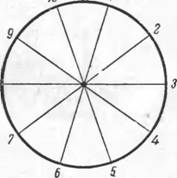
На концах пяти диаметров все порядковые числа от 1 до 10 расположены так, как показано на рис. 24. При таком расположении только в одном случае сумма двух

соседних чисел равна сумме двух противоположно расположенных чисел, а именно:

10+1 = 5 + 6, но, например,

1+2 ! = 6 + 7,

или

2 + 3 ! = 7 + 8.

Перерасположите данные числа так, чтобы сумма любых двух соседних чисел равнялась сумме соответствующих двух противоположно расположенных чисел.

Можно ожидать, что эта задача имеет не одно решение, то есть разные расположения данных чисел удовлетворяют условию задачи.

Попытайтесь найти такой путь решения задачи, который позволил бы установить и число всех возможных решений.

10 1