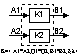Конечным автоматом называется формальная система К которая задается 5-ю объектами К=<A, Q, B, d, l >, где A — входной алфавит ={a₁, a₂, a₃, …, a_m}, Q — алфавит состояний {q₁, q₂, q₃, …, q_n}, B — выходной алфавит {b₁, b₂, b₃, …, b _k}, d — функция переходов; d: Q?A®Q ; l — функция выходов автомата ; l: Q?A®B .

1). КА — это модель дискретного преобразователя данных.

2). КА функционирует во времени.

3). Возможно различное соединение автоматов.

Сетью из автоматов называется соединение автоматов таким образом, что выходы одних служат входами других и все автоматы в сети функционируют одновременно (согласованно).

Замечание : для описания сети из автоматов надо ввести понятие времени, т.к. важно знать в каких состояниях находится каждый из автоматов сети и в какие моменты времени.

Основные виды соединения : 1). Параллельное, с общим и с раздельным входом.

2). Последовательное K=< A1;Q1*Q2;B2;d;l>

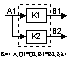
3). Соединение с обратной связью K=< A1*B1;Q1;d;l>

Представленных 3-х видов соединения достаточно для построения любой автоматной сети.

Способы введения времени в автоматную сеть: 1). Синхронный: а). Вводиться шкала времени , которая делиться на отрезки одинаковой длины ( такты), которые нумеруются с 0. б). Длина такта принимается за единицу измерения времени в). Входные и выходные строки a= ai1,ai2, … , aik ; b=bj1, bj2, … , bjk ; bj?B , ai?A рассматриваем как последовательность знаков сменяемых каждый такт. г). Автоматные функции реализуются с задержкой q(t)?Q , a(t)?A , b(t)?B , t?{0,1, … ,}? N; d:(q(t), a(t))=q(t+1) автомат Мили : l(q(t),a(t))=b(t) ; автомат Мура l(q(t),a(t))=b(t+1) д). Синхронизация работы автоматов в сети достигается за счет: внешнего источника синхронизации; идеальных временных характеристик среды и автоматов. 2). Асинхронный. Определение: состояние qi является устойчивым по входному знаку aj, если d(qi, aj)=d(qi, aj aj). В асинхронном автомате любое состояние устойчиво по любому входному знаку ведущему в это состояние.