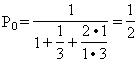Зная размеченный граф состояний системы, легко написать систему алгебраических уравнений для предельных вероятностей состояний и рассчитать их. Но если две системы имеют одинаковые графы состояний и различаются лишь интенсивностями потоков, то нет надобности каждый раз выписывать системы этих уравнений.

Рассмотрим так называемый “процесс гибели и размножения”, который лежит в основе изучения простейших систем массового обслуживания.

Марковская непрерывная цепь называется “процессом гибели и размножения”, если граф состояний имеет вид, представленный на рис. 1.6, т.е. все состояния можно вытянуть в одну цепочку, в которой каждое из средних состояний связано прямой и обратной связью с каждым из соседних состояний, а крайнее состояние только с одним соседним состоянием.

Запишем для вероятностей состояний систему уравнений и решим её.

Для первого состояния X₁ имеем:

?₀₁P₀=?₁₀P₁

Для второго состояния X₂ имеем:

?₀₁P₀+?₂₁P₂=?₁₀P₁+?₁₂P₁ , но ?₁₂P₁=?₂₁P₂ , тогда

?₂₁P₂=?₁₂P₁

Аналогично получаем:

?₂₃P₂=?₃₂P₃

…………………

?_k-1,kP_k-1=?_k,k-1P_k

…………………

?_n-1,nP_n-1=?_n,n-1P_n

Итак, предельные вероятности состояний P₀ , P₁ , ………. , P_n в любой схеме гибели и размножения удовлетворяют системе:

?₀₁P₀=?₁₀P₁

?₁₂P₁=?₂₁P₂

?₂₃P₂=?₃₂P₃

_{………………………}

?_k-1,kP_k-1=?_k,k-1P_k

_{………………………}

?_n-1,nP_n-1=?_n,n-1P_n и

условию: P₀+P₁+………+P_n=1.

Решим систему следующим образом: из первого уравнения выразим P₁ :

Из второго, с учётом предыдущего равенства, получим :

и т.д.

Для

Эта формула справедлива для любого

Полученные значения P₁……..P_n подставим в уравнение

P₀+P₁+………+P_n=1.

Получим :

Откуда:

Зная P₀ , найдём все остальные значения вероятностей P₁ , P₂ , …… , P_n по вышеприведённым формулам. Таким образом, задача «гибели и размножения» решена в общем виде.

Пример 1.3. Найти предельные вероятности состояний для процесса «гибели и размножения», размеченный граф состояний которого изображён на

рис. 1.7.

;

Проверим: