В рассмотренных ранее примерах предполагалось, что временем передачи сигнала от входа объекта к выходу можно пренебречь. Это будет справедливо, если время передачи сигнала значительно меньше наибольшей постоянной времени системы. Однако на практике так бывает не всегда. Ряд объектов, например, трубопровод, ленточный конвейер и т.д., не отвечают изложенным выше предположениям. Для того чтобы учесть время передачи сигнала в структурную схему дополнительно вводится гипотетически существующее звено чистого запаздывания.

Звеном чистого запаздывания называется звено, выходной сигнал которого, в точности повторяет входной сигнал с задержкой на время t. Передаточная функция такого звена имеет вид: W(p)=e^—pt, где t — время задержки.

Для анализа устойчивости систем, содержащих звено чистого запаздывания, в силу трансцендентности характеристического уравнения, нельзя использовать алгебраические критерии. Поскольку звено чистого запаздывания не влияет на устойчивость разомкнутой системы, то при анализе устойчивости разомкнутых систем звено чистого запаздывания игнорируют, но при анализе устойчивости замкнутых систем так поступать нельзя. Рассмотрим один из способов анализа устойчивости замкнутых систем, содержащих звено чистого запаздывания.

Структурная схема системы представлена на рис. 5.8.

Рис. 5.8. Система, содержащая звено чистого запаздывания.

Пусть разомкнутая система является устойчивой. Построим для нее частотный годограф без учета влияния звена чистого запаздывания.

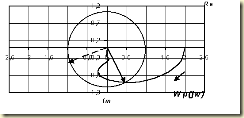
Рис. 5.9. Частотный годограф разомкнутой системы, содержащей звено чистого

запаздывания, t=0.

Пример частотного годографа разомкнутой системы приведен на рис. 5.9. На рисунке также нанесена окружность единичного радиуса с центром в начале координат. При построении годографа влияние звена чистого запаздывания не учитывалось. При некоторой частоте w_кр, годограф пересекает окружность. Вектор комплексного коэффициента передачи, соответствующий частоте w_кр, также изображен на рис. 5.9. Построенный нами радиус-вектор характеризует комплексный коэффициент передачи на частоте w_кр – его амплитуду (модуль вектора) и фазу (угол поворота вектора относительно действительной оси). Звено чистого запаздывания не оказывает влияния на величину выходного сигнала, следовательно, на модуль вектора оно не влияет, изменится только угол поворота вектора на величину —w_крt. То есть, вследствие влияния звена чистого запаздывания, наш радиус-вектор повернется по часовой стрелке дополнительно на угол w_крt. Возможное влияние звена чистого запаздывания демонстрирует пунктирный радиус- вектор. Если с учетом влияния звена чистого запаздывания, радиус — вектор будет принадлежать 3-му (как в нашем примере) или 4-му квадранту, то в соответствии с 1-й формулировкой критерия Найквиста, замкнутая система будет устойчивой. Если же поворот радиус-вектора будет столь велик, что он перейдет в 2-й или 1-й квадрант, то частотный годограф охватит точку –1,0 и замкнутая система будет неустойчива.

Подводя итог нашим рассуждениям, сформулируем этапы решения подобного рода задач:

1) решить уравнение и вычислить частоты, при которых годограф пересекает окружность единичного радиуса (т.е. w_кр), причем, следует учитывать только физически реализуемые значения частот, т.е. неотрицательные, положительные;

2) проверить выполнение условия , если оно выполняется, то замкнутая система будет устойчивой.

Пример 5.5.

Найти, при каких значениях t система с будет устойчива, если k=5, T=0.1. Найдем действительную и мнимую части комплексного коэффициента передачи разомкнутой системы: .

Тогда:

.

Уравнение принимает вид: , и его корни могут быть найдены как . Подставим значения k и T: . Отбрасывая физически нереализуемую отрицательную частоту, получим .

Найдем рад. Теперь проверим выполнение условия : . Поскольку , то замкнутая система будет устойчивой.