Пусть имеется линейная система, характеристическое уравнение которой имеет вид:

A(p)=a_npⁿ+a_n-1p^n-1+…+a₀=0. Перейдем от комплексной переменной p к мнимому выражению jw, тогда наше выражение А(р) принимает вид A(jw)=a_n (jw)ⁿ+a_n-1 (jw)^n-1+…+a₀, где величина w может рассматриваться как частота. Изменяя 0 <w< ?, построим годограф Михайлова – геометрическое место точек конца вектора A(jw), при изменении частоты от 0 до ?.

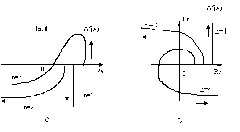Рис. 5.2. Примеры годографов Михайлова – а) неустойчивых систем; б) устойчивых систем.

Формулировка критерия Михайлова:

Для устойчивости линейной системы автоматического управления необходимо и достаточно, чтобы годограф Михайлова, начинаясь на действительной, положительной полуоси при изменении w от 0 до ?, последовательно, в положительном направлении (против часовой стрелки) обходил n квадрантов, где n- порядок характеристического уравнения.

Пример 5.3.

Определим с помощью критерия Михайлова устойчивость системы, рассмотренной в примере 5.1. Характеристическое уравнение этой системы:

. (5.10)

Зададим следующие значения параметров системы: k=10, T₁=0,5, T₂=0,1. В этом случае наше уравнение принимает вид:

. (5.11)

Перейдем от p к jw, тогда: , откуда:

. (5.12)

Выделим действительную и мнимые части A(jw):

; .

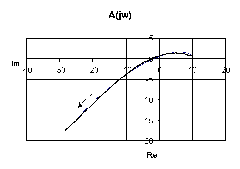
Меняя w в достаточно широких пределах, строим годограф Михайлова (см. рис. 5.3). Как видно из рис. 5.3, годограф Михайлова последовательно обходит 1-й, 2-й и 3-й квадранты. Порядок исследуемой системы равен 3, следовательно, она устойчива.

Рассмотрим систему, описываемую в разомкнутом состоянии следующей передаточной функцией: , где K— некоторое постоянное число. Обычно оно имеет физический смысл коэффициента усиления.

Рис. 5.3. Годограф Михайлова для примера 5.3.

Тогда для замкнутой системы: . Вид годографа Михайлова замкнутой системы, очевидно, будет определяться полиномом D(p), а величина слагаемого K будет задавать величину смещения годографа вдоль действительной оси.

Пример 5.4.

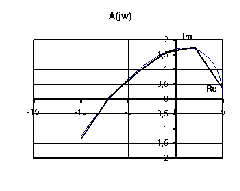
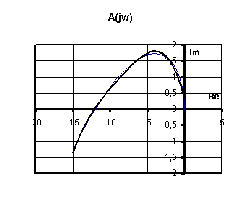
Рассмотрим объект из примера 5.1. Зададим следующие значения параметров системы: T₁=0,5, T₂=0,1, и построим годограф Михайлова для двух значений K (см. рис. 5.4).

а) б)

Рис. 5.4. Годограф Михайлова для примера 5.4: а) K=5; б) K=0.

Как видно из рис. 5.4, мнимая ось сдвигается влево на величину K. Очевидно, что увеличение коэффициента усиления K не влияет на устойчивость системы, пока выполняется неравенство K<K_kp. Величина ?K_kp? может быть определена из рис. 5.4,б как координата пересечения годографа с действительной осью. В нашем примере K_kp»12.