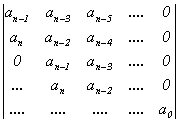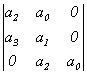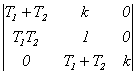Пусть имеется линейная система, характеристическое уравнение которой имеет вид:

a_npⁿ + a_n-1p^n-1 +…+ a₀ = 0. (5.1)

Составим из коэффициентов уравнения a_i, определитель Гурвица по следующему правилу:

— расположим на главной диагонали коэффициенты a_i, начиная с a_n-1;

— ниже главной диагонали расположим коэффициенты a_i, последовательно увеличивая индекс на единицу, если будут получены несуществующие индексы, пишем ноль;

— выше главной диагонали расположим коэффициенты a_i, последовательно уменьшая индекс на единицу, если будут получены несуществующие индексы, пишем ноль (5.2).

(5.2)

Формулировка критерия Гурвица:

Для устойчивости линейной системы автоматического управления необходимо и достаточно, чтобы при a_n>0 все главные диагональные миноры определителя Гурвица были положительны.

Если все главные диагональные миноры положительны, а один из них равен 0, то система является нейтральной.

Пример 5.1.

Рассмотрим систему, описываемую следующей структурной схемой:

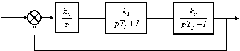Рис. 5.1. Структурная схема к примеру 5.1.

Здесь k₀, k₁, k₂ – коэффициенты усиления, а T₁, T₂ – постоянные времени.

Найдем передаточную функцию разомкнутой системы: .

Тогда передаточная функция замкнутой системы:

. (5.3)

Откуда характеристическое уравнение системы:

=0, где k = k₀k₁k₂. (5.4)

Построим определитель Гурвица сначала в общем виде для n=3, затем подставив значения коэффициентов характеристического уравнения получим:

(5.5)

Здесь имеют место следующие значения коэффициентов характеристического уравнения: , , , .

Проверим, выполняются ли условия критерия Гурвица:

— , так как постоянные времени (в нашем случае это T₁ и T₂) всегда положительны, то это требование выполняется автоматически;

— найдем первый главный диагональный минор определителя Гурвица:

, это неравенство будет выполняться всегда по той же причине, что и рассмотренное выше;

— найдем второй главный диагональный минор определителя Гурвица:

, это неравенство не очевидное, преобразуем его: ; поскольку коэффициенты усиления (в нашем случае это k) по своей физической природе положительны, то это неравенство принимает вид:

. (5.6)

— найдем третий главный диагональный минор – это сам определитель Гурвица:

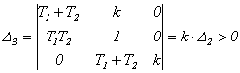; поскольку k по своей физической природе больше нуля, то это неравенство сводится к виду: , которое уже рассмотрено нами выше.

Таким образом, исследуемая система будет устойчива, если будет выполняться неравенство (6.6).

Следствие из критерия Гурвица:

Для систем порядка меньше 3 положительность коэффициентов характеристического уравнения является необходимым и достаточным условием устойчивости системы.

Рекомендуется читателю в качестве упражнения самостоятельно доказать это положение. Критерий Гурвица не рекомендуется применять при n>6 , так как возникают трудности с вычислением определителей высокого порядка.