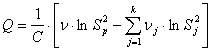Цель работы: Привить навыки по обработке экспериментальных данных, представленных несколькими выборками сравнительно небольшого объема, доказательства гипотез о равенстве их средних арифметических и дисперсий, а также о возможносьти их объединения в одну выборку суммарного объема.

Ход работы:

2.1.Сравнение центров двух выборочных распределений

Из исходной выборки выделяем с помощью таблицы равномерно распределенных случайных чисел две частные выборки, объемами n₁=12 и n₂=16.

n₁: 4.408; 6.108; 5.370; 4.874; 4.560; 4.981; 4.496; 4.748; 4.795; 4.816; 5.192; 4.661.

n₂: 4.290; 4.640; 4.874; 5.266; 4.452; 5.784; 5.091; 5.13; 5.041; 4.452; 4.216; 4.56; 4.795; 5.13; 4.481; 4.722.

Докажем для эти выборок статистическую неразличимость (различимость) средних арифметических. Т.е. необходимо принять или опровергнуть следующие гипотезы:

H₀: = или H₁:. Для этого нам необходимо вычислить и , а также эмпиричнские дисперсии и . В качестве критерия берется t-распределение стьюдента: , где средневзвешенная дисперсия с числом степеней свободы , а n₁ и n₂ – соответствующие объемы выборок. В нашем случае n₁=12 и n₂=16. , =0,199089, =0,161589, =4,917267, =4,807631. После вычислений получим: t=1,609094 , а t_таб = 2,0639. Т.к. t < t_таб , то мы принимаем гипотезу о статистической неразличимости средних арифметических этих выборок.

2.2. Сравнение выборочных дисперсий

По данным двух выборок находим эмпирические дисперсии =0,199089 с числом степеней свободы , и =0,161589 с числом степеней свободы . В этом случае нулевая гипотеза, подлежащая проверке, запишется как H₀:= , а альтернативная ей H₁: .

Для проверки нулевой гипотезы составлляем дисперсионное отношение , которое представляет собой F-распределение Фишера; F = 1,232067. F_таб=2,54 при , а . Т.к. F < F_таб , то мы принимаем нулевую гипотезу, т.е. гипотезу о равенстве выборочных дисперсий.

2.3. Объединение выборок

Т.к. было одновременно доказаны статистическая неразличимость дисперсий и средних арифметических данных двух выборок, то мы имеем право объединить их в одну. При этом параметры объединенной выборки м.б. подсчитаны непосредственно или по формулам:

, где

, , — среднее арифметическое, выборочная дисперсия и объем j-й выборки соответственно.

Параметры объединенной выборки, подсчитанные непосредственно:

, .

Параметры объединенной выборки, подсчитанные по формулам:

, .

Сравнение полученных результатов показывает, что средние арифметические совпадают полностью.

2.4. Метод Тьюки

Из исходной выборки выделяем с помощью таблицы равномерно распределенных случайных чисел четыре частные выборки (k=4), объемами n=6 каждая.

Таблица1.

Выбоки n₁ n₂ n₃ n_4.

n1	n2	N3	n4
4,805	5,555	5,008	4,981
4,540	4,595	4,965	4,356
5,501	4,922	4,847	5,113
5,130	4,938	4,309	5,141
5,370	4,356	4,309	4,748
5,091	5,186	4,462	4,661

2.5. Доказательство статистической неразличимости (различимости)

средних арифметических этих выборок

Вычисляем средние арифметические и эмпирические дисперсии полученных выборок:

Таблица 2.

Значения и .

номер выборки	1	2	3	4
	5,073	4,925	4,650	4,833
	0,105139	0,14973	0,089178	0,076697

Т.к. выборки взяты из нормальных совокупностей, то сущуствует некоторый интервал TS, внутри которого центры выборок статистически неразличимы.

, где — стьюдентизированный размах..

— средняя выборочная дисперсия с числом степеней свободы.

Для нашего случая имеем: ; ; .

Сопоставив найденный интервал с данными выборок, мы увидим, что все цениры выборок попадают в интервал статистической неразличимости.. Следовательно гипотеза о статистической неразличимости средних арифметических этих выборок принимается.

2.6. Доказательство статистической неразличимости

(различимости) выборочных дисперсий

Доказательство сводится к проверке нулевой гипотезы H₀: . Т.к. число выборок k=4 > 2, а объем каждой выборки n=6 одинаков, то для проверки нулевой гипотезы используем критерий Кохрена, который основан на законе распределения отношения максимальной эмпирической дисперсии к сумме всех дисперсий, т.е.

.

Это распределение имеет степени свободы , где n- объем одной выборки и , где k-число выборок; и меняется в пределах 0 < G < 1. По выбранному уровню значимости q и степеням свободы и выбираем табличное значение .

Для нашего случая имеем: ; . Т.к. , то принимается нулевая гипотеза H₀: , т.е. доказана статистическая неразличимость выборочных дисперсий.

2.7. Объединение выборок

Т.к. было одновременно доказаны статистическая неразличимость дисперсий и средних арифметических данных выборок, то мы имеем право объединить их в одну. При этом параметры объединенной выборки м.б. подсчитаны непосредственно или по формулам, привиденных в п 2.3.

Параметры объединенной выборки, подсчитанные непосредственно:

, .

Параметры объединенной выборки, подсчитанные по формулам:

, .

Сравнение полученных результатов показывает, что средние арифметические и дисперсии совпадают полностью.

2.8. Доказательство статистической неразличимости (различимости)

эмпирических дисперсий 6 выборок и поиск средневзвешенной дисперсии

Т.к. мы имеем частные выборки неодинакового объема, то для доказательство статистической неразличимости (различимости) эмпирических дисперсий этих выборок применим критерий Бартлетта.

,

где — поправочный коэффициент.

— средневзвешенная дисперсия; — число степеней свободы всех выборок;

и — дисперсия и число степеней свободы j — й выборки.

Для нашего случая имеем: С = 1,062389 ; ; ; ; ?²_таб=1,15.

Т.к. Q < ?²_таб , то все дисперсии признаются статистически неотличимыми друг от друга и равными величине .

2.9. Сравнение эмпирических дисперсий частных выборок

Таблица 3.

Значения дисперсий выборок.

выборки	n1=12	n2=16	n3=6	n4=6	n5=6	n6=6	n1+n2=28			N=200
дисперсии	0,1991	0,16156	0,10514	0,14973	0,08918	0,07670	0,18060	0,12870	0,142	0,34061
относитель-ная ошибка	30,715	30,7145	30,7145	30,7145	21,0352	18,0775	14,6490	13,5333	9,87248	5,00877

При выборках малого объема чрезмерно велики ошибки (статистический разброс), особенно дисперсий, что может приводить к неточностям при принятии решений, а то и прямо к неверны решениям.

2.10. Определение границ существования МО

Таблица 4.

Значения границ существования МО

Объём	Среднее	Дисперсия	t(табл.)	нижняя	Верхняя
6	5,073	0,105139	2,5706	4,732583	5,41315
6	4,925	0,14973	2,5706	4,519168	5,331332
6	4,650	0,089178	2,5706	4,336409	4,963191
6	4,833	0,076697	2,5706	4,542614	5,123886
12	4,9172667	0,199089	2,201	4,633767	5,200767
16	4,8076313	0,161589	2,1314	4,593435	5,021827
24	4,855	0,180604	2,0687	4,675163	5,034073
28	4,87029	0,156708	2,045	4,717303	5,023281
52	0	0,142	2,008	-0,10493	0,104932
200	5,049	0,340606	1,9749	4,967316	5,130316

По данной таблице можно сделать вывод, что с увеличением объема выборки величина доверительного интервала уменьшается.

ВЫВОД: В процессе лабороторной работы мы привили навыки по обработке экспериментальных данных, представленных несколькими выборками сравнительно небольшого объема, доказательства гипотез о равенстве их средних арифметических и дисперсий, а также о возможносьти их объединения в одну выборку суммарного объема.