Цель работы: Выработать навыки по обработке полученных экспериментальным путем статистических данных для определения характеристик случайных величин и выявления степени точно­сти их определения, нахождения теоретического закона распределения случайных вели­чин и применения его в статистических расчетах.

 

Ход работы

Начальные данные: имеется выборка из 200 эксперементальных данных. Обработав ее имеем сле­дующие результаты.

1.1. Построение гистограммы распределения

Max значение в выборке Xmax = 6.879.

Min значение в выборке Xmin = 3.6783.

Количество разрядов гистограммы: К=9 вычисляем по формуле , N – объем выборки.

Шаг гистограммы вычисляем по формуле 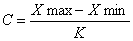= 0.3556.

Центры разрядов вычисляем по формуле: , где j = 1,2, … ,k.

Для нашей выборки имеем:

Таблица 1. Значения центров и разрядов гистограммы.

центры	1	2	3	4	5	6	7	8	9
разряды	3,856117	4,21175	4,567383	4,923017	5,27865	5,634283	5,989917	6,34555	6,701183

Вычислим количество попаданий в интервалы: , где j = 1,2, … ,k.

Таблица 2. Количество попаданий в границы интервалов.

интервалы	Границы интервалов	попадания
нижняя	верхняя
1	3,6783	4,033933	6
2	4,033933	4,389567	13
3	4,389567	4,7452	43
4	4,7452	5,100833	50
5	5,100833	5,456467	44
6	5,456467	5,8121	26
7	5,8121	6,167733	9
8	6,167733	6,523367	5
9	6,523367	6,879	4

Строим гистограмму и полигон выборочного распределения. Высота столбцов соответствует количеству попаданий в каждый из 9 интервалов:

Рис.1. Гистограмма и полигон выборочного распределения.

1.2. Нахождение оценок основных параметров ряда распределения

Для нахождения моментов 1,2,3 и 4 порядков использую ниже написанную формулу:

, где , .

Первый центральный момент равен 0.

Второй центральный момент называется дисперсией распределения и часто обозначается . Среднеквадратическое отклонение можно вычислить по формуле: .

Для наших данных имеем следующие результаты (центральные моменты):

Таблица 3. Значения центральных моментов.

Первый	Второй (дисперсия)	Третий	Четвертый
0	0,335	0,0975	0,3752

Основные моменты представляют собой отношение центральных моментов к среднеквадратическому отклонению в соответствующей степени:

, в частности: ; ; ; ; .

Для нашего случая получаем следующие результаты:

Таблица 4. Значения основных моментов.

Порядок	0	1	2	3	4
Значение	1	0	1	0,244	0,375

Третий основной момент служит мерой косости (асимметрии) кривой распределения относительно центра:

, .

Выражение служит мерой крутости (эксцессом) выборочного распределения относительно кривой нормального распределения. Так как ?>0 (? = 0,346), то кривая распределения более круто уходит вверх, чем нормальное распределение и является островершинной.

При статистических расчетах в силу конечного числа опытов, большое значение имеют основные ошибки вычисления всех параметров ряда распределения. Находим их по следующим формулам:

, ; ; .

По нашим данным имеем следующие значения:

Таблица 5. Значения ошибок вычислений.

0,040907	0,0289	0,173	0,346

Одним из наиболее грубых методов доказательства того, что исследуемая случайная величина распределения по нормальному закону, является проверка следующих выражений:

и .

В нашем случае получаются следующие результаты:

1. первое условие выполняется, следовательно, выборочное распределение подчиняеться нормальному закону;

2. второе условие верно, что подтверждает подчинение выборочного распределения нормальному закону.

Точность проведенных вычислений можно охарактеризовать обобщающим параметром, который называется показателем точности исследования:

,

При подстановке наших значений, имеем следующие результаты: .

Ниже приведу все вычисленные данные:

:

; ;

; ;

; .

1.3. Выбор теоретической кривой распределения и доказательство

ее правильности (неправильности)

Для высказывания гипотезы о нормальном распределении можно воспользоваться критерием согласия Пирсона. Для этого необходимо построить таблицу Пирсона.

1. Найдем выравнивающие частоты, то есть те частоты, которые должны быть при нормальном распределении для тех же аргументов, для которых у нас уже имеются выборочные частоты. Это наиболее просто подсчитать по формуле:

,

где — центрированный нормированный аргумент, — масштабируемое число, которое служит для приведения теоретических значений нормального распределения к масштабу нашего опыта. Совмещаем на одном графике выборочные и выравнивающие частоты.

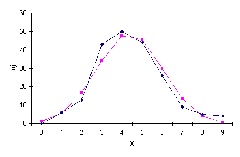Рис. 2. Частоты выборочного (1) и выравнивающего (2) распределения.

Таблица 6. Таблица Пирсона:

j
0	3,50048	-2,693	0	1,306317	0,13459
1	3,856	-2,07804	6	5,6621164
2	4,212	-1,463	13	16,817125	0,8664
3	4,567	-0,848	43	34,226888	2,24874
4	4,923	-0,234	50	47,733779	0,10759
5	5,279	0,381	44	45,617023	0,05732
6	5,634	0,996	26	29,872447	0,502
7	5,989	1,6108	9	13,404709	1,44736
8	6,346	2,226	5	4,1217978	2,94939
9	6,701	2,8404	4	0,8684778
10	7,0568	3,4552	0	0,12539
?			200	199,6306	8,1788

Так как критерий Пирсона требует, чтобы количество наблюдений составляло не менее 5, поэтому мы объединяем некоторые ячейки. После окончательных расчетов получим, что по критерию Пирсона величина c² составляет 8.58585. При объединении рядов их количество уменьшилось по сравнению с первоначальным и составит .

Количество степеней свободы можно найти по формуле: . В нашем случае получим следующие данные:

, и .

Но такое значение не дает возможности с уверенностью утверждать или отрицать гипотезу. Существует простое правило (критерий Романского), значительно облегчающее применение критерия Пирсона:

.

В нашем случае имеем , следовательно, расхождение между выборочными и выравнивающими частотами можно считать случайными, а выборочный ряд подчиняющимся нормальному закону.

1.4. Определение аналитического выражения функции

плотности вероятности и поля допуска

Так как мы доказали, что гипотеза о нормальном распределении не противоречит данным опыта, то можно воспользоваться теоретическим выражением функции плотности вероятности:

,

подставляя в которое оценочные параметры, имеем:

Определим вероятность попадания исследуемой величины в любой наперед заданный интервал значений по формуле:

,

подставив в данную формулу наши данные (для 7 и 8 интервалов) получим, что . Для сравнения подсчитаем суммарную частость (относительную частоту) в том же интервале, определенные прямо на гистограмме: ,

объяснения разности двух значений можно найти, посмотрев на график частот выборочного и выравнивающего распределения (кривые частот выборочного и выравнивающего распределения на 7 и 8 интервалах расходятся).

Поле допуска случайной величины при заданной вероятности можно определит по формуле:

.

Полученные результаты привожу в следующей таблице:

Таблица 7. Поля допусков для заданных вероятностей.

Pдов	0.80	0.90	0.997
	4,31659	4,10777	3,32281
	5,79973	6,00855	6,7935
	0,74157	0,95039	1,73534

ВЫВОД: В результате проведенной работы я получил навыки по обработке данных, полученных экспериментальным путем, научился находить характеристики случайных величин и выявлять степени точности их определения, находить теоретический закон распределения случайных величин и применять его в статистических расчетах.