Рассмотренные ранее положения и выкладки, справедливы лишь в случае нормального распределения контролируемого параметра. Между тем, при практических применениях, иногда возникает ситуация, когда это требование не выполняется. Рассмотрим кратко пути выхода из этой ситуации.

Если закон, которому подчиняется контролируемый параметр, известен, то можно подобрать преобразование, приводящее его к нормальному виду (см. [5, с. 32]). Теоретически для любого унимодального закона такое преобразование может быть найдено. В этом случае, необходимо, используя найденное преобразование, пересчитать экспериментально полученные данные и уже по пересчитанным данным строить контрольные карты. Этот путь очень трудоемок, так как требует большого количества вычислений, что в цеховых условиях не всегда возможно.

Можно пойти по иному пути. Как известно [4, c. 239] средние арифметические распределены асимптотически нормально. Следовательно, если мы будем применять КК «в лоб», не преобразуя экспериментальные данные, то чем больше объем мгновенной выборки, тем ближе закон распределения выборочных средних приближается к нормальному. Главным недостатком такого подхода является необходимость увеличения объема мгновенных выборок, что не всегда экономически приемлемо.

В ряде случаев, когда закон распределения исследуемого параметра асимметричен, поступают следующим образом:

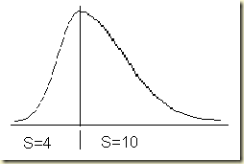
1. Разбивают закон распределения контролируемого параметра на две части, каждую из которых можно рассматривать, как половину некоторой кривой нормального закона. В результате исходный закон представляется в виде суммы двух половинок различных нормальных кривых, обладающих разными дисперсиями, но одинаковым центром (см. рис. 1.6).

2. Для каждой части исходного распределения находят свои границы регулирования, в зависимости от величины дисперсии соответствующего ей нормального распределения.

В результате мы получим контрольную карту, имеющую несимметричные границы регулирования (см. рис. 1.7).

Рис. 1.6. Пример несимметричного распределения

Пример несимметричного закона распределения приведен на рис. 1.6. Видно, что это закон может быть представлен в виде суммы половинок двух кривых нормального распределения с различными дисперсиями. Так левая часть закона может быть представлена как левая половинка кривой нормального закона, у которой стандартное отклонение равно 4, а правая часть закона – как правая половинка кривой нормального закона, у которой стандартное отклонение равно 10.

Рис. 1.7. Контрольная карта, построенная для параметра, подчиняющегося закону распределения, изображенному на рис. 1.6.

Пример контрольной карты, построенной для контролируемого параметра, закон распределения которого изображен на рис. 1.6, представлен на рис. 1.7. Видно, что верхняя граница регулирования, которой соответствует большая дисперсия, удалена от центра распределения значительно дальше, чем нижняя граница, которой соответствует меньшая дисперсия.