При построении контрольных карт индивидуальных значений объем мгновенной выборки принимается равным единице. Через некоторые промежутки времени (обычно они постоянны) производится измерение контролируемого параметра, и полученный результат наносится на контрольную карту в виде точки. Если точка выходит за границы технологического допуска, то это свидетельствует о разладке ТП.

При построении КК индивидуальных значений (в дальнейшем – ККХ) требуется, чтобы контролируемый параметр подчинялся нормальному закону распределения. Если это требование не выполняется, то выводы сделанные по КК Х, могут оказаться неверными.

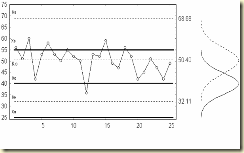Рис. 1.2. Контрольная карта индивидуальных значений

Различают статистические границы регулирования, которые будем обозначать как К_н и К_в, и технологические границы – Х_н, Х_в. Статистические границы рассчитываются исходя из экспериментальных данных и требуемой вероятности изготовления годных изделий, а технологические границы — задаются в технологической документации. Необходимо так настроить ТП, чтобы эти границы были как можно ближе друг к другу.

Пример графика, построенного при использовании ККХ, приведен на рис. 1.2. Здесь пунктиром обозначены статистические границы регулирования, а непрерывной линией – технологические границы и их центр. Справа от КК представлены предполагаемый закон распределения контролируемой величины (непрерывная кривая), и реальный закон распределения (пунктирная кривая).

Для того чтобы вычислить значения статистических границ регулирования поступают следующим образом:

, (1.1)

, (1.2)

где: — среднее арифметическое контролируемой величины,

— ее стандартное отклонение,

— величина, извлекаемая из табл. 1.1, которая определяется заданной вероятностью изготовления годных изделий Р_дов.

По полученным экспериментальным данным можно рассчитать статистические границы регулирования. В нашем случае , а , тогда:

К_в=50,6+3*5,88=57,64; К_н=50,6-3*5,88=22,36;

(расчет проведен для Z_дов=3, что соответствует Р_дов=0,9973).

Таблица 1.1

Зависимость Z_дов от величины Р_дов

Рдов как функция от Zдов		Zдов как функция от Рдов
1-Рдов	Рдов	Zдов		Zдов	1-Рдов	Рдов
1	0,00	0,0000		0,0	1,00000	0,00000
0,95	0,05	0,0627		0,2	0,84148	0,15852
0,90	0,10	0,1257		0,4	0,68916	0,31084
0,85	0,15	0,1891		0,6	0,54851	0,45149
0,80	0,20	0,2533		0,8	0,42371	0,57629
0,75	0,25	0,3186		1,0	0,31731	0,68269
0,70	0,30	0,3853		1,2	0,23014	0,76986
0,65	0,35	0,4538		1,4	0,16151	0,83849
0,60	0,40	0,5244		1,6	0,10960	0,89040
0,55	0,45	0,5978		1,8	0,07186	0,92814
0,50	0,50	0,5745		2,0	0,04550	0,95450
0,45	0,55	0,7554		2,2	0,02781	0,97219
0,40	0,60	0,8416		2,4	0,01640	0,98360
0,35	0,65	0,9346		2,6	0,00932	0,99068
0,30	0,70	1,0364		2,8	0,00511	0,99489
0,25	0,75	1,1503		3,0	0,00270	0,99730
0,20	0,80	1,2816		3,2	0,00137	0,99863
0,15	0,85	1,4395		3,4	0,00067	0,99933
0,10	0,90	1,6449		3,6	0,00032	0,99968
0,05	0,95	1,9600		3,8	0,00014	0,99986
0,01	0,99	2,5758		4,0	0,00006	0,99994
0,001	0,999	3,8906

Примечание: Р_дов — вероятность изготовления годного изделия,

1- Р_дов – вероятность изготовления бракованного изделия.

Видно, что статистические границы не совпадают с границами технологического допуска. Это приводит к заметному количеству бракованных изделий. Так, при Z_дов=3, доля годных изделий должна составить 0,9973 в нашем же случае она составит:

, что соответствует почти 23% брака (здесь Ф(·)-интеграл Лапласа).

Очевидно, что ширина двух законов распределения – постулируемого и реального — близка друг к другу, однако центры расположены непозволительно далеко, что неизбежно приводит к большой доле брака. Это подтверждается и самой контрольной картой, на которой центр статистических границ регулирования К₀ не совпадает с центром технологического допуска Х₀. Вывод – ТП должен быть налажен с тем, чтобы совместить центры технологического допуска и статистических границ регулирования. В этом случае величина брака может быть значительно снижена.

Если отцентрировать ТП при неизменной величине разброса контролируемого параметра, то для данных нашего примера вероятность изготовления годных деталей составит: , что соответствует всего 1,2% брака.

Как правило, при использовании КК границы регулирования устанавливаются для Z_дов=3 (так называемые трехсигмовые границы). В этом случае вероятность изготовления бракованных изделий составит 0,27%, что более чем достаточно для современного производства. В дальнейшем, если не оговорено противное, мы будем использовать статистические границы регулирования, вычисленные для Z_дов=3. Все таблицы, приведенные в этой работе, с помощью которых определяют границы регулирования для любых видов контрольных карт, вычислены для трехсигмовых границ.

В том случае, если трехсигмовые границы, по каким-либо причинам нас не устраивают (например, мы задаемся другим значением Р_дов), значения, извлекаемые из таблиц, нужно пересчитать. Для этого нам необходимо поделить табличное значение на 3 (это значение Z_дов, для которого построены таблицы) и умножить на значение Z_дов, соответствующее выбранной нами величине Р_дов, извлеченной из табл. 1.1.

Труд, затраченный на сбор информации, проведение вычислений и составление контрольной карты, может быть сведен на нет отсутствием сопутствующей информации. Так, необходимо кроме самих значений контролируемой величины зафиксировать – вид изделия, название технологической операции, наименование контролируемого параметра, используемый измерительный прибор, название цеха, бригады, номер смены, фамилию контроллера, дату и время проведения измерения и т.д. Отсутствие этой информации делает работу по составлению КК бесполезной. Поэтому для практических применений используют специально разработанные бланки контрольных карт, пример которой, представлен на рис. 1.3.

Здесь информация, которая заносится на карту вручную (за исключением самого графика), выделена курсивом. На бланк контрольной карты заранее наносятся и подписываются границы технологического допуска Х_в и Х_н, а также его центр Х₀.

Одной из трудностей, с которыми сталкиваются при практическом применении ККХ — это интерпретация результатов контроля.

Дело в том, что теоретически, нормальное распределение имеет бесконечные «хвосты», следовательно, точка на ККХ вне контрольных пределов не всегда свидетельствует о действительной разладке ТП. Для того чтобы уменьшить вероятность ошибочного принятия решения о наладке ТП, используются карты средних арифметических и медиан.