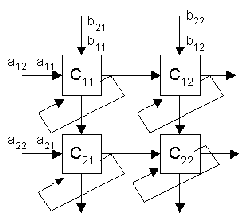Заданы две матрицы и . Пусть известно, что надо найти матрицу , равную произведению матриц и , и известен элемент матрицы:

Запишем рекуррентное выражение:

,

.

Как только у нас появилось рекуррентное выражение или система рекуррентных выражений такого типа, то мы можем представить это вычисление в виде систолической структуры, где . Рисуем структуру ПЭ:

Рис.7.23.

Всего будет три регистра, умножитель и сумматор.

Видно, что отразили рекуррентное выражение в структуру ПЭ. А т.к. это конвейерное устройство, то каждое поступаемое данное подаем для временного хранения в буферный регистр.

А теперь хотим организовать так, чтобы каждая итерация реализовывалась своим ПЭ: сколько итераций – столько ПЭ. Нарисуем процессорную матрицу для случая n=2:

.

Изображаем четыре ПЭ: с₁₁, с₁₂, с₂₁, с₂₂.

Рис.7.24.

Для того чтобы эта систолическая структура смогла правильно вычислить произведение мы должны подавать элементы на вход в нужное время и в нужной последовательности:

В результате получили следующую систолическую структуру: подавая нужные данные в нужное время, мы как бы вычисляем в каждом ПЭ элемент результирующего произведения.

К перемножению м-ц на систолической структуре требует тактов работы. На последовательной ЭВМ требуется выполнить команд.

Для представления систолических структур используется описание ПЭ и граф систолической матрицы и структуры.