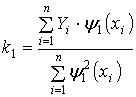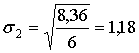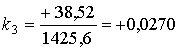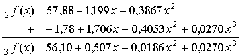На практике часто встречаются случаи, когда необходимо найти уравнение какой-либо переменной (случайной величины) от другой случайной величины, числовые значения которой равноотстоящие друг от друга, то есть, соблюдается равенство

X₂ — X₁=X₃ — X₂=…=X_n — X_n-1= DX . (2.38)

Это могут быть задачи об изменениях цен, урожая, количества осадков и т.п. по годам или любые другие задачи, лишь бы соблюдалось равенство (2.38). В этом случае легко весь класс таких задач свести к единому аргументу, преобразовав именованные случайные величины X_i в абстрактные номера интервалов x_i

, (2.39)

где X_н = X_min — DX – начальные значения аргумента.

Для решения таких задач П.Л. Чебышев предложил простой способ отыскания функции

f(x) = k₀ + k₁y₁(x) + k₂y₂(x) + … + k_ly_l(x) , (2.40)

где l ? n-1, причём n — количество интервалов;

;

;

;

;

;

;

;

— — — — — — — — — — — — — — —

.

Согласно формуле (2.40) первый член суммы является средним арифметическим выборки по случайной величине Y, первые два члена представляют собой линейное уравнение, три члена – квадратичное и т.д. Прибавляя к функции по одному новому члену мы увеличиваем степень уравнения на единицу. Для практических целей достаточно параболы 2-го или 3-го порядка, поэтому дальнейшие разложения полинома y_l(x) здесь не приводятся.

Наилучшая кривая сглаживания считается полученной при достижении минимума ошибки приближения параболы

, (2.41)

где ;

.

Проверку полученного уравнения на степень приближения к экспериментальным данным можно вести по критерию c²-Пирсона, методика работы с которым изложена в разделе 1.3.

Пример 5. По числовой выборке середины разрядов табл.2.1 найти уравнение связи по методу параболического сглаживания и определить степень его достоверности.

Р е ш е н и е: Для нахождения уравнения связи воспользуемся формулами (2.40)-(2.41). Результаты вычислений для удобства будем записывать в специальную таблицу.

0) Вычисление параболы нулевого порядка.

;

;

;

.

1) Вычисление параболы первого порядка.

;

;

;

При сложении первого и второго члена суммы (2.40) получается:

;

.

Так как s₁<s₀, то вычисления следует продолжать.

2) Вычисление параболы второго порядка.

;

;

;

При сложении третьего члена суммы (2.40) с предыдущими получается:

;

;

.

Так как s₂<s₁, то вычисления следует продолжать.

3) Вычисление параболы третьего порядка.

;

;

;

При сложении четвёртого члена суммы (2.40) с предыдущими получается:

;

.

Последовательность вычислений параболического сглаживания

для равноотстоящих значений аргумента

xi	Yi	y1i	Yiy1i	y2i	Yiy2i	y3i	Yiy3i	2f(x)	3f(x)
1	56,8	-4	-227,2	+9,333	+530,1	-16,8	-954,24	57,07	56,62
2	59,7	-3	-179,1	+2,333	+139,3	+8,4	+501,48	57,03	57,26
3	59,1	-2	-118,2	-2,667	-157,6	+15,6	+921,96	57,76	58,18
4	60,7	-1	-60,7	-5,667	-344,0	+10,8	+655,56	59,27	59,56
5	60,8	0	0	-6,667	-405,4	0	0	61,55	61,55
6	65,6	+1	+65,6	-5,667	-371,8	-10,8	-708,48	64,61	64,30
7	69,5	+2	+139,0	-2,667	-185,4	-15,6	-1084,20	68,44	68,00
8	74,5	+3	+223,5	+2,333	+173,8	-8,4	-625,80	73,04	72,79
9	79,3	+4	+317,2	+9,333	+740,1	+16,8	+1332,24	78,41	78,84
	586	—	+160,1	—	+119,1	—	+38,52	2c2=0,272	3c2=0,252
	38636,62	60	—	308,000	—	1425,6	—	Р(2c2)=0,99951	Р(3c2)=0,99967

Так как s₃>s₂, то вычисления прекращаются и формально наилучшим считается уравнение второго порядка. Однако в силу того, что s₂»s₃ это ещё надо доказать. С этой подсчитаем значения функций ₂f(x) и ₃f(x) (см. таблицу), а затем по выражению (1.21) определим для каждого из уравнений величину c², по которой найдём вероятность правильной аппроксимации. Для нашего примера это Р(₂c²)=0,99951 и Р(₃c²)=0,99967. Так как табл.П.1 для такой точности не приспособлена, то пришлось воспользоваться таблицами в [4]. Такие вероятности означают, что с точностью до 0,1% оба уравнения равноценны. В этом случае предпочтение нужно отдавать простейшему из них

,

которое, при подстановке первичного преобразователя 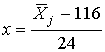превращается в обычное регрессионное уравнение

.

Сравнение этого уравнения с ранее найденными показывает практически полное его совпадение с М2 табл.2.3 и некоторое незначительное отличие (в пределах исследованного диапазона ) с уравнением, полученным в примере 1 раздела 2.2.