Этапы проектирования дискретных устройств:

1. Системное (архитектурное) проектирование.

2. Логический (синтез).

3. Технический.

На системном этапе осуществляется декомпозиция вычислительного средства (как программной,так и аппаратного) на части (на сеть слабо взаимодействующих автоматов более простой структуры).

Системное проектирование. Этап неформализуемый, а потому описание этих автоматов неформализованное. Исходные данные для этого этапа-класс решаемых задач характеристики вычислительного средства как то: стоимость, быстродействие, результат. Общая блок схема ВС-словесное описание.

Методы проверки результатов проектирования — программное моделирование.

Логическое проектирование (ЛП). При ЛП осуществляется формализация описания составных частей средства и его синтез с целью получения логических (функциональных схем).Исходные данные -описания функционирующих блоков частей .

Результатом является логическое или функционирующие схемы.

Метод: теория автоматов.

Логический этап разделяется на:

1. Формализация

2. Структурный синтез (каноническая схема синтеза)

Технический проект. На основе логических и функциональных схем строятся принципиальные и монтажные схемы и готовится технологическая документация производства и эксплуатации программного средства.

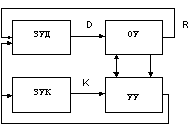
Декомпозиция дискретных преобразователей по Глушкову.

Произвольный КА может быть декомпозирован на 2 слабо взаимодействующих автомата: Операционные устройства и Управляющее устройство.

Арифметические основы операционных автоматов.

Для того чтобы ОА по Глушкову работал, нужна внешняя память, т.к. неограниченную память, как в МТ, сделать сложно, мы представим, что данные хранятся в запоминающем устройстве команд (ЗУК).

Должны предусмотреть такие операции, чтобы класс решаемых задач был как можно больше.

Требования к операционному устройству (ОУ) является реализация функционально полного набора операций.

Мы должны реализовать ОА к произвольной системе дискретных функций.

Арифметическая логика.

В булевой алгебре {+,-,*} является функционально полной.

Легко доказать, что арифметический базис в К-значной логике также является функционально полным. Для этого необходимо выразить {min,max,~} через {+,-,*}.