M – множество исходных сообщений.

I – множество смыслов.

a — правило интерпретации.

b — правило обработки сообщений.

b’- правило обработки информации

a,a’-деклоративные знания, b’,b — процедурные знания, причем b — это алгоритм, а b’- то, что мы думаем об b.

Тема 1.1 Программная реализация автоматов.

Операция – дискретная функция,зависящая от всех своих переменных.

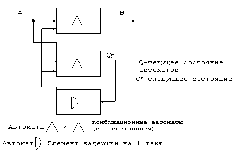
Схема синтеза конечных автоматов (КА) Хафмена-Глушкова.

Под синтезом КА будем понимать представление КА в виде сети или схемы автоматов элементарной структуры.

Есть 2 подхода:

1. Алгебраическая теория автоматов (автоматы с памятью).

2. Комбинаторная теория автоматов.

Автоматы с памятью – автоматы,у которых количество состояний больше единицы.

В комбинаторной теории элементарных автоматов,из которых синтезируются автоматы произвольной сложности,используются элементарные задержки на один такт и элементарный комбинационный автомат.

В алгебраической теории доказано, что задача синтеза является алгоритмически неразрешимой, т.е. для произвольного множества автоматов с памятью невозможно доказать является ли это множество автоматов.

Схема синтеза Хафмена-Глушкова относится к комбинаторной теории автоматов и основывается на основной теореме структурного синтеза автоматов.

Теорема:

Произвольный КА может быть представлен сетью из трех автоматов:

Комбинационные автоматы

Комбинационный автомат – это автомат, реализующий дискретную функцию.

Комбинационный автомат – это КА с 1 состоянием.

A	Q	Q’
…	…	…

—количество двоичных разрядов

n=3 1<<2

—количество двоичных разрядов для А

m=4 =2

Пример таблицы истинности ,

A	Q	Q’
X1	X0	Y1	Y0	Z1	Z0
0	0	0	0	*	*
0	0	0	1	*	*
…	…	…	…	…	…
1	1	1	0	*	*

Элемент D:в нем появляется необходимость, когда нужно создать синхронный автомат, а так в нем необходимости нет.