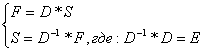Любая ЦОС основана на разложении произвольной функции сигнала в ряд по некоторой системе ортогональных функций. Например, функции cos и sin являются ортогональными и можно разложить произвольную функцию в ряд по этим функциям. Оказывается некий произвольный сигнал мы можем представить в виде композиции более простых сигналов. Обобщая это можно записать, что произвольную функцию f(t) можно представить в виде ряда некоторой ортогональной функции, но в связи с тем, что мы не можем обрабатывать бесконечные ряды, поэтому мы вынуждены ограничить число членов в этом ряду. А в этом случае мы теряем точность, но так как у нас уже задана разрешающая способность, то мы можем ограничиться числом членов в этом ряду, чтобы остаточный член этого ряда был меньше, чем наша разрешающая способность. И, как следствие этого, мы записываем не бесконечную, а конечную функцию.

где Q и t – это ортогональные функции, по которым раскладывается произвольная функция;

S_i – коэффициенты разложения или же совокупность таких коэффициентов составляет спектр сигнала по системе функций Q(i,t). Для того чтобы мы могли переходить от спектра к сигналу и от сигнала к спектру мы должны иметь возможность вычислять эти коэффициенты. Поэтому мы должны иметь возможность вычислить эти коэффициенты:

,

то есть система функций будет тогда ортогональна, когда мы, зная отсчеты сигналов в дискретные моменты времени сможем получить спектр этого сигнала, вычисляя указанную сумму.

Условие ортогональности следующее:

где

но так как мы работаем не с функцией, а с отсчетами, поэтому эта первая сумма будет равна какому-то отсчету в момент времени t, где t – это число от 0 до К-1, где К – число отсчетов сигнала или объем выборки.

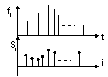
Как найти К? Частота дискретизации известна; можем посчитать длительность выборки; можем найти объем выборки, а объем выборки и есть К, то есть сколько точек мы должны одновременно обработать. В виде графика это выглядит следующим образом:

есть функция f(t), заданная отсчетами и путем вычисления этой суммы получаем спектр сигнала. Если в качестве ортогональных функций использовать sin или cos, то получается Фурье-спектр. Но кто сказал, что не существует других функций кроме sin и cos, для того чтобы эти функции удовлетворяли приведенному ниже дискретному условию ортогональности. Оказывается таких функций достаточно много. Выражения, которые составляют дискретные ортогональные преобразования можно записать в матричном виде:

Таким образом, задачи цифровой обработки сигналов мы можем свести к матричным вычислениям. Нам требуется решения следующих задач: умножение вектора на матрицу и обращение матриц.