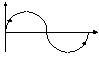
Если частотный спектр сигнала f(t) ограничен некоторым значением F, то этот сигнал может быть восстановлен после дискретизации без погрешностей по выборочным значениям, следующим с интервалом .

Физический смысл теоремы Кательникова очень прост: если у нас имеется в спектре сигналов максимальная гармоника, которая отлична от нуля, равная частоте F, то для того чтобы мы смогли восстановить и частоту этой гармоники и ее амплитуду надо как минимум 2 точки. Поэтому мы должны оцифровывать сигнал с частотой превосходящей двойную частоту спектра. На практике интервал времени Dt мы должны выбирать меньше чем тот, который может быть получен из теоремы Кательникова: .

Нарисуем таблицу.

Сигнал	Частота дискретизации(Гц)	Длительность выборки(сек)	разрядность	Объем выборки
Измерительные	10?103	100?10	22?12	10-1?105
Речевые	104?105	1?10-1	14?8	103?105
Изображение	106?108	10-2?10-3	8?4	104?106

Оказывается, в зависимости от полосы частот, которые занимают эти сигналы, могут быть подсчитаны следующие диапазоны дискретизации, которые используются в этих прикладных областях.

Квантование – это процесс преобразования выборочных значений сигнала в последовательность отсчетов. Идея здесь следующая: мы получаем решетчатую функцию, а это означает, что она принимает значение в диапазоне от минимального до максимального. Но так как в реальных системах у нас всегда задана некая точность измерения ( обработки, восприятия), а это означает, что мы можем задать точность d с которой мы будем обрабатывать наш сигнал. Более того, из-за наличия шумов мы принципиально не можем эту точность устремить к нулю. Поэтому если мы зададим некую точность d, или ее еще называют разрешающей способностью обработки, то это означает, что наш диапазон от f_min до f_max разбивается на N частей и значение функций принадлежащей какой-то из этих частей будет нами отождествлено числом, равным номеру этого интервала. Заранее понятно, что мы не можем обрабатывать данные со сколь угодно большой точностью. Значит разрешающая способность любой технической системы ограничена. Отсюда следует, что число разрядов, с помощью которых мы должны закодировать полученные выборочные значения, может быть представлена, как целая часть от величины:

.

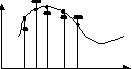
Заметьте, у нас тогда были выборочные значения, а после квантования они называются отсчеты сигналов.

Реальный отсчет сигнала может быть или больше или меньше выборочного значения на величину не более половины разрешающей способности.

«Точкой» обозначены выборочные значения. «Полочкой» обозначены отсчеты сигналов.

Разрядность уменьшается из-за того, что объем данных растет, а объем данных связан с таким параметром, как длительность выборки, которая подлежит обработке. Мы должны входные данные делить на части и эти части обрабатывать. А если это так, то исходя из предметных областей есть параметр, называемый длительностью выборки и равен КDt, где К – это число отсчетов сигналов, которые подлежат одновременной обработке.

Длительность выборки должна быть такая, чтобы задержка на это время не вызывала особых слуховых эффектов.

Относительная ошибка, которая получается в результате квантования есть . Абсолютная ошибка квантования: . При проектировании систем ЦОС добиваются, чтобы эта ошибка была по уровню сигнала не более заданной.