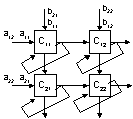1. Символьная обработка: поиск вхождения подстроки в строку.

Предположим у нас имеется 2 строки: А=а₁,а₂,а₃…а_n и В=b₁,b₂,b₃,…b_m причем n>m. Ставится задача поиска вхождения строки В в строку А. Оказывается этих точек вхождения может быть не одна. Упростим задачу и будем считать, что b_i и а_i это двоичные цифры, то есть а_i??0,1?, b_i??0,1,??. Результат мы должны получить в следующем виде: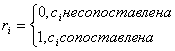

Эта задача решается с помощью линейной систолической структуры. Нарисуем эту структуру.

У нас будет 5 ПЭ. На эту систолическую структуру мы будем подавать данные в разных направлениях. Приведем временную диаграмму функционирования этой системы. Будем предполагать что n=5, а m=3.

В первый момент времени считаем, что никаких данных не содержится, то есть поступает а₁, далее ничего не содержится, а в конце b₁. В следующий момент

Что мы видим: если мы начнем сопоставлять знаки, то окажется, что если мы результат сопоставления представим в булевом выражении и выполним конъюнкцию, то у нас в этом случае будет r0, здесь будет r1, а здесь r2. Таким образом, используя эту линейную систолическую структуру за n тактов мы получаем результат сопоставления за однократный просмотр. Здесь фактически увеличили в 2 раза объем данных, а время при этом увеличилось в 2 раза. Теперь представьте себе, что длина этой матрицы 2Кб. И у нас здесь не биты, а ПЭ сравнивания знаков(символов). И у нас линия не в один проводник, а в 8 или 16, если 16-ти битовая значимость. Вот вам система для сравнения, сопоставления, в том числе и с учетом знаков. Видно, что для каждой задачи требуется создать свою систолическую структуру и разработать свой алгоритм.

Каждый ПЭ может выполнять операции сравнения битов(слов) и накапливать результаты сравнения через 1 такт, используя операцию логического умножения.

Рассмотрим 2-ой алгоритм:

2. Умножение квадратных матриц.

Заданы 2 матрицы А и В. Предположим известно, что надо найти матрицу С равную произведению матриц А и В. И известен элемент матрицы: Запишем рекуррентное выражение:

c_ij(0)=0

c_ij(k)=c_ij(k-1)+a_ikb_kj

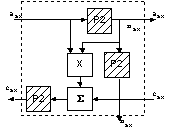
Как только у нас появилось рекурентное выражение или система рекурентных выражений такого типа, то мы можем представить это вычисление в виде систолической структуры, где . Рисуем структуру ПЭ:

У нас будет 3 регистра, умножитель и сумматор.

Видно, что отразили рекуррентное выражение в структуру ПЭ. А так как это конвейерное устройство, то каждое поступаемое данное подаем для временного хранения в буферный регистр.

А теперь хотим организовать так, чтобы каждая итерация реализовывалась своим ПЭ: сколько итераций – столько ПЭ. Нарисуем процессорную матрицу для случая n=2: 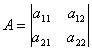. Рисуем 4 ПЭ: с₁₁, с₁₂, с₂₁, с₂₂.

Для того чтобы эта систолическая структура смогла правильно вычислить произведение мы должны подавать элементы на вход в нужное время и в нужой последовательности: а11-b21;a12-b22.

Вот получили такую систолическую структуру: подавая нужные данные в нужное время, мы как бы вычисляем в каждом ПЭ элемент результирующего произведения.

К перемножению матриц nxn на систолической структуре требует n^2 тактов работы. На последовательной ЭВМ требуется выполнить n^3 команд.

Систолические алгоритмы найдены для широкого спектра задач числовой обработки данных, обработки сигналов, символьной обработки: умножение, обращение матриц, решение линейной систем уравнений, дискретное преобразование Фурье, кодирование, декодирование числовых последовательностей.

Для представления систолических структур используется описание ПЭ и граф систолической матрицы и структуры. Y=AX X=A^-1Y

Задача 3: Решение систем линейных уравнений

Задан ПЭ и используется гексагональная структура. Осей – 3, то есть данные прокачиваются как бы в 3 направлениях.