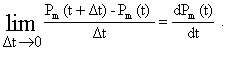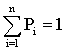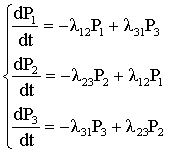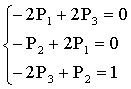Рассмотрим некоторую систему S с дискретными состояниями Х₁ , Х₂, … , Х_n ,которая переходит из состояния в состояние под влиянием некоторых потоков событий. Будем считать, что эти потоки простейшие. Тогда вероятность Р_ij перехода из состояния Х_i в состояние Х_j , за малый промежуток времени Dt равна l_ijDt , т.е. Р_ij = l_ijDt , где Р_ij называется переходной вероятностью, а l_ij — плотностью потока, переводящего систему из состояния Х_i в состояние Х_j . Предполагая, что известны плотности вероятностей перехода l_ij , построим граф состояний системы и над дугами напишем соответствующие плотности l_ij . Такой граф называется размеченным графом состояний. Оказывается, что, зная этот размеченный граф, можно определить вероятности состояний P₁(t) , P₂(t), … , P_n(t), как функция времени.

Для описания процессов с непрерывным временем используем модель в виде так называемой марковской цепи с дискретным состоянием, считая время непрерывным. В этом смысле будем говорить, что имеем дело с непрерывной марковской цепью.

Рассмотрим однородный процесс, т.е. процесс, в котором l_ij не зависит от t .

Пусть система в некоторый момент времени t находится в состоянии Х_m с вероятностью P_m(t) . Придадим величине t малое приращение Dt и найдем вероятность того, что в момент времени t + Dt система будет находиться в том же состоянии Х_m . Это событие может произойти следующим образом: 1) в момент t система уже была в состоянии Х_m и за время Dt не вышла из этого состояния или: 2) в момент t система была в состоянии Х_{i ,} а за время Dt перешла в состояние Х_m . Вероятность первого варианта вычисляется так: P_m(t) умножается на условную вероятность того, что система за Dt не перейдет ни в какое другое состояние Х_i (i?m) . Так как события, состоящие в переходе за время Dt из Х_m в Х_i , несовместны, то вероятность того, что осуществится один из этих переходов, равна сумме их вероятностей, т.е.

(с точностью до бесконечно малых высших порядков).

Вероятность того, что не осуществится ни один из этих переходов, равна

Отсюда вероятность первого варианта

P_m(t) ( ) .

Аналогично, вероятность второго варианта равна вероятности того, что в момент t система была в состоянии Х_i (i?m), умноженной на условную вероятность перехода за время Dt в состояние Х_m :

P_i (t) ·l_im·Dt

Применяя правило сложения вероятностей, получим:

P_m(t+Dt) = P_m(t) ( ) + =

P_m(t) (1 — l_m1Dt — l_m2Dt — … — l_mnDt) + P₁(t) l_1mDt +

+ P₂(t)l_2mDt + … + P_n(t)l _nmDt ;

P_m(t+Dt) — P_m(t) = P₁(t) l_1mDt + P₂(t)l_2mDt + … + P_n(t)l _nmDt —

— P_m(t) l_m1Dt — P_m(t) l_m2Dt — … — P_m(t) l_mnDt .

Последнее равенство делим на Dt , получим

P₁(t) l_1m + P₂(t)l_2m + … + P_n(t)l _nm —

-P_m(t) l_m1 — P_m(t) l_m2 -…- P_m(t) l_mn ;

Перейдем к пределу при Dt ® 0

При этом правая часть уравнения не изменится, поскольку она не зависит от Dt .

Таким образом, дифференциальное уравнение имеет вид:

Аналогичные уравнения можно записать для всех вероятностей состояний P_i (t) , и все вместе они составят систему уравнений, которые носят название уравнений Колмогорова.

Интегрирование этой системы с учетом условий

дает все вероятности состояний.

Поскольку совместно с этим условием число уравнений для определения вероятностей составляет n+1 , то одно любое из дифференциальных уравнений системы всегда можно опустить.

Обратим внимание на структуру уравнений Колмогорова. Все они построены по вполне определенному правилу, которое можно сформулировать следующим образом:

В левой части каждого уравнения стоит производная вероятности состояния, а правая часть содержит столько членов, сколько переходов связано с данным состоянием. Если переход направлен из данного состояния, то соответствующий член имеет знак »минус», если в данное состояние – знак »плюс». Каждый член равен произведению плотности вероятности соответствующего перехода, умноженной на вероятность того состояния, из которого исходит переход.

Пример 1.1. Составим систему уравнений Колмогорова для случая, когда граф состояний имеет вид, представленный на рис.1.4.

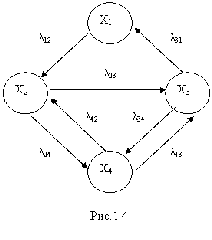Пользуясь приведенными выше правилами, получаем систему дифференциальных уравнений Колмогорова:

К этим уравнениям надо добавить еще начальные условия.

Например, если при t = 0 система S находится в состоянии Х₁ , то начальные условия имеют вид:

P₁ (0) = 1; P₂ (0) = P₃ (0) = P₄ (0) = 0 .

Далее поставим вопрос следующим образом: что будет происходить в системе S при t ® ? ? Будут ли функции P₁ (t) , P₂ (t) , … , P_n (t) стремиться к каким-то пределам ?

Если число состояний системы конечно и граф состояний системы является сильно связным (из любого состояния система может перейти в любое другое), то можно доказать, что пределы вероятностей состояний, которые назовем предельными вероятностями состояний, существуют и не зависят от начального состояния системы, т.е.

Предельные вероятности состояний в сумме должны давать единицу.

Таким образом, при t ® ? каждое состояние системы осуществляется с постоянной вероятностью, т.е. в системе устанавливается так называемый стационарный режим .

Для вычисления предельных вероятностей состояний P₁ , P₂ , … , P_n , необходимо в системе уравнений Колмогорова положить все левые части равными нулю, так как в стационарном режиме все вероятности состояний постоянны, а это значит, что их производные равны нулю. Система уравнений Колмогорова превращается в систему линейных алгебраических уравнений, решив которую, найдем P₁ , P₂ , … , P_n .

Пример. 1.2. Система имеет возможные состояния Х₁ , Х₂ , Х₃ , размеченный граф которой дан на рис.1.5.

Запишем уравнения Колмогорова для вероятностей состояний:

Полагая левые части первых трех уравнений равными нулю, получим

Поскольку одно уравнение можно опустить, рассмотрим систему из 2-х первых уравнений и, учитывая, что P₁ + P₂ + P₃ = I , получаем систему

Из первых 2-х уравнений имеем

Из уравнения -2Р₁ + 2 Р₃ = 0 Р₃ = Р_{1 .} Подставим в уравнение Р₁ + Р₂ + Р₃ = 1

Р₃ + 2Р₃ + Р₃ = 1; 4Р₃ = 1 ; Р₃ = ; Р₁ = , Р₂ = .

Таким образом, предельные вероятности состояний равны:

Р₁ = ; Р₂ = ; Р₃ = . Это означает, что в стационарном режиме система S будет проводить в состоянии Х₁ в среднем часть времени, в состоянии Х₂ – половину времени и в состоянии Х₃ — часть времени.