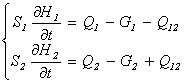При рассмотрении любой задачи управления необходимо предварительно рассмотреть объект управления. Состояние объекта управления характеризуется целым рядом величин. Одни из них измеряются в процессе управления и называются контролируемыми. Другие величины, которые оказывают влияние на объект, но не измеряются, называются неконтролируемыми. Воздействия, не зависящие от системы управления, называются возмущениями. Как правило, выделяют два вида возмущений:

— возмущения нагрузки;

— помехи.

Всякий объект управления имеет изменяющуюся во времени нагрузку, т.е. от этих возмущений он не может быть избавлен. Наличие помех связано с различными побочными явлениями и нежелательными эффектами. Чем ниже уровень помех, тем лучше для объекта управления.

Контролируемые величины, значения которых задаются системой управления, называются управляющими величинами, величины относительно которых сформулирована задача управления, называются управляемыми.

Величины, воздействующие на объект, показаны на рис. 1.1.

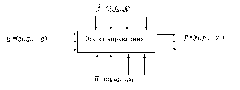Рис. 1.1. Воздействия, поступающие на вход объекта управления.

Здесь использованы следующие обозначения:

— вектор неконтролируемых возмущений; — вектор контролируемых возмущений; — вектор управляющих воздействий; — вектор управляемых величин.

Введем еще один вектор =(x₁, x₂,…, x_n), компонентами которого являются величины, однозначно характеризующие состояние объекта. В дальнейшем будем называть координаты векторов и управляющими и управляемыми координатами, соответственно, а координаты векторов и — координатами внешних воздействий, координаты вектора — координатами состояния.

Если известно математическое описание объекта, то известна и система уравнений, связывающая управляемые величины со всеми внешними воздействиями. Объекты, которые имеют одну управляющую и одну управляемую величину называются простыми или односвязными, если же объект имеет несколько управляющих и управляемых величин, то его называют многосвязным.

В том случае, если контролируемые координаты однозначно определяют состояние объекта, то говорят, что объект полностью наблюдаем. Объект называют полностью управляемым, если с помощью управляющих воздействий можно однозначно задать состояние объекта. Если объект описывается системой линейных дифференциальных уравнений, то объект называют линейным. В том случае, если он описывается нелинейными дифференциальными уравнениями, то его относят к классу нелинейных объектов.

Различают статические и динамические характеристики объекта. В первом случае внешние управляемые и неуправляемые воздействия не зависят от времени, и нас интересует статическая характеристика управления, которая описывает зависимость управляемых координат от управляющих координат . Если же рассматривается зависимость управляемых координат от изменяющихся во времени управляющих координат, то говорят о динамических характеристиках объекта.

Объект управления может быть устойчивым, неустойчивым и нейтральным. Объект устойчив, если после кратковременного внешнего воздействия его состояние с течением времени возвращается к исходному. Устойчивые объекты также называют объектами с самовыравниванием. Состояние неустойчивого объекта, после окончания внешнего воздействия продолжает изменяться, удаляясь от первоначального состояния. Нейтральные объекты, после окончания внешнего воздействия, стабилизируются в некотором состоянии равновесия, отличном от исходного. Такие объекты также называются объектами без самовыравнивания.

Один и тот же объект, имеющий нелинейную характеристику, может, в зависимости от режима работы, находиться в устойчивом, нейтральном или неустойчивом состоянии.

Пример 1.1.

Рассмотрим в качестве примера объекта управления гидравлический резервуар, изображенный на рис. 1.2.

Рис. 1.2. Гидравлический резервуар

Здесь приняты следующие обозначения:

Q — объем воды, притекающей в резервуар;

G — объем воды, вытекающей из резервуара;

H — уровень воды в резервуаре;

S — площадь поперечного сечения резервуара.

Поведение исследуемого объекта может быть описано следующим дифференциальным уравнением:

(1.1)

В качестве управляющей величины можно рассматривать Q, а в качестве возмущения — G. Состояние объекта характеризуется величиной H, которая и является управляемой величиной. Рассматриваемый объект является односвязным, так как у него одна управляющая и одна управляемая величина. При кратковременном изменении величины Q объект перейдет в новое устойчивое состояние, характеризуемое новым значением величины H. Отсюда можно сделать вывод, что рассматриваемый объект нейтрален.

Пример 1.2.

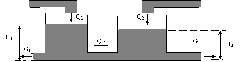В качестве примера двусвязного объекта, рассмотрим два сообщающихся резервуара, представленных на рис. 1.3.

Рис. 1.3. Сообщающиеся резервуары

Здесь введена функция Q₁₂(H₁—H₂) описывающая зависимость объема перетекающей жидкости из одного сосуда в другой от разности уровней жидкости в этих резервуарах, которая в общем случае является нелинейной. Поведение объекта описывается следующей системой дифференциальных уравнений:

(1.2)

Рассматриваемая система является двухсвязной, так как имеет две управляющие (Q₁,Q₂) и две управляемые (H₁,H₂) величины. Иными словами, вектора и имеют следующий вид:

; . (1.3)

В качестве компонент вектора состояния , характеризующего состояние объекта, могут быть выбраны компоненты вектора , т. е. = = (H₁, H₂).

Для сложных объектов, математическое описание может принимать различный вид в зависимости от того, какие параметры контролируемые, а какие нет, какие параметры изменяются во времени, а какие остаются неизменными. Таким образом, можно сделать вывод, что математическое описание конкретного объекта зависит от решаемой задачи управления.

Задачи, поставленные перед системой управления, могут быть разбиты на следующие группы:

1. Задачи стабилизации, когда необходимо с заданной точностью поддерживать постоянными те или иные выходные величины.

2. Программное управление, когда закон изменения управляемой величины заранее известен и не зависит от конкретного значения возмущающих воздействий.

3. Слежение, когда управляемая (выходная) величина воспроизводит некоторую функцию измеряемой величины.

4. Адаптация системы на оптимальное значение одного или нескольких параметров системы. В этом случае система управления при выработке управляющих воздействий должен учитывать опыт предыдущей эксплуатации объекта.

По реализованному в них принципу автоматического управления системы управления (в дальнейшем СУ) разбиваются на группы — разомкнутые и замкнутые.

В разомкнутых системах управляющее воздействие задается без учета действительного значения управляемой величины, на основании измеренных внешних воздействий. В этом случае говорят о жестком управлении, а сам принцип регулирования называют регулированием по возмущению.

В замкнутых системах управляющее воздействие формируется на основании измеренного значения управляемой величины. Данный принцип управления называют регулированием по отклонению.

Рассмотрим примеры реализации различных принципов регулирования.

В описанном ранее гидравлическом резервуаре будем контролировать расход жидкости G, то есть внешнее возмущение. Зная G и Q, вычислим H. Задача, поставленная перед системой управления (в дальнейшем СУ) — поддержание уровня жидкости в некотором заданном диапазоне. Система регулирования по G и Q вычисляет, необходимое для решения поставленной задачи значение Q, и устанавливает его. Это пример регулирования по возмущению. Легко видеть, что если наш объект будет иметь неконтролируемые возмущения (например, течь в резервуаре), то решить поставленную задачу СУ не сможет. Изменим СУ. Будем измерять непосредственно значение выходной величины (в нашем случае — H). В зависимости от разности H—H₀ (где H₀ — требуемое значение H), система изменяет величину Q, и решает, таким образом, поставленную перед ней задачу. Это пример регулирования по отклонению.