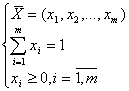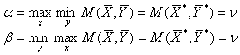В экономике при планировании и управлении, в военном деле часто встречаются ситуации, которые носят конфликтный характер. Такие ситуации имеют лица, интересы которых частично или полностью противоположны. И возникает задача выбора рациональной обработки действий участников конфликта для достижения поставленной цели. Эта задача отличается от ранее рассмотренных экстремальных задач, в которых имелось одно лицо, заинтересованное в достижении поставленной цели. Необходимость анализировать, разрешать подобные ситуации привела к созданию теории игр. Возникновение теории игр относится к 1941 году когда была опубликована монография «Теория игр и экономическое поведение».

Теория игр – это математическая теория конфликтных ситуаций. Задача теории игр – это выработка рекомендаций по рациональному образу действий участников конфликта. Так как математика изучает не сами явления (не конфликты), а их модели, то необходимо построить математические модели конфликтных ситуаций. Итак, в теории игр рассматриваются математические модели конфликтных ситуаций. Такую модель называют игрой. Игра отличается от реальной конфликтной ситуации тем, что ведется строго по определенным правилам, чего в конфликтной ситуации может и не быть. Человек издавна знаком с моделированием конфликтных ситуаций – игр. Например: шашки, шахматы. В любой из этих игр имеются участники. Исход игры кончается выигрышем (проигрышем) кого-то из участников. Для достижения своей цели у участников игр имеется определенный набор действий, которые они выполняют. Вся терминология игр идентична терминологии математических игр. Участники конфликта называются игроками. Исход конфликта (исход игры) называется выигрышем или ценой игры. Для достижения своей цели каждый из участников конфликта имеет в наличии определенные действия, которые называются стратегиями игроков. Выбор игроком своей стратегии называется ходом. Ходы бывают личные и случайные. Личный ход осуществляется с помощью различных действий самого игрока. Случайный ход осуществляется с помощью действий какого-либо механизма. В рулетке все ходы случайные. В карточных играх –часть ходов личные, часть случайные.

Существует 2 способа задания игры:

1. Нормальный

2. Позиционный

Позиционный способ связан с развернутой формой игры и сводится к графу последовательных шагов, к дереву игры.

Нормальный способ заключается в явном представлении стратегий игроков и некоторой функции, номер для каждой сов-ти стратегий игроков определяет размер выигрыша (проигрыша) каждого из игроков. Такая функция называется платежной. Каждый из игроков стремится к тому, чтобы как можно больше выигрыш или меньше проигрыш. Стратегия игрока называется оптимальной, если она при многократном повторении игры обеспечивает игроку максимальный средний выигрыш или минимальный средний проигрыш.

Рассмотрим краткую классификацию игр:

1. Игры бывают по числу ходов:

· Одноходовые

· Многоходовые

2. По числу количества стратегий у игроков:

· Конечные

· Бесконечные

3. По числу участников:

· Парные

· Множественные

4. По характеру игры:

· Неантогонистические

· Антогонистические

5. По способу игроков в коалиции:

· Коалиционные

· Некоалиционные

Платежная матрица.

Рассмотрим игру двух игроков A и B. Игра антогонистическая и выигрыш одного из игроков является проигрышем другого.

Сумма выигрыша равна нулю, поэтому такую игру называют игрой двух лиц с нулевой суммой. Будем условно считать, что игрок A-выигрывающий, B-проигрывающий. У игрока A для достижения целей имеется m частных стратегий A_1, A_2…. A_m,

У игрока B — n частных стратегий B_1, B_2….B_n Задана платежная функция, которой каждой паре стратегий (A_i,B_j) ставит в соответствие некоторое число , i=1,m , j=1,n. Это число является выигрышем игрока A.

Матрица C=( C_ij)_m?n называется платежной матрицей. Ее будем задавать в виде таблицы:

	B1	B2	—	Bj	—	Bn
A1	C11	C12	—		—
A2	C21	C22	—		—
—	—	—	—	—	—	—
Ai	Ai1	Ci2	—	Cij	—	Cin
—	—	—	—	—	—	—
Am	Cm1	Cm2	—	Cmj	—	Cmn

Строки – чистые стратегии игрока A, столбцы — чистые стратегии игрока B.

Если игрок A выбирает стратегию A_i , а B — B_j , то выигрыш игрока A есть число C_ij .

Примеры игр:

О завозе товара в магазин.

На базе торговой организации имеется 4 типа товаров, а в магазин можно завести один из них. Если товар типа j будет пользоваться спросом, то магазин получит прибыль от его реализации P_j. Если он спросом пользоваться не будет, то убытки от его порчи и хранения l_j . Требуется выбрать такой тип товара, который целесообразно завести в магазин.

Пусть значения прибыли и убытка в таблице:

J	1	2	3	4
Pj	25	26	23	20
lj	10	8	6	4

Построить платежную матрицу. Будем считать, что спрос на товар не известен. Пусть магазин будет игрок. А , тогда у него 4 стратегии:

А₁— завести товар 1 типа

А₂ — завести товар2 типа

А₃ — завести товар 3 типа

Игроком В будет спрос на товар

В₁ – спрос на товар 1 типа

В₂ – спрос на товар 2 типа

В₃ – спрос на товар 3 типа

	В1	В2	В3	В4
А1 А2 А3 А4	25 -8 -6 -4	-10 26 -6 -4	-10 -8 23 -4	-10 -8 -6 20

2). Игра “заяц — контролер”

Будем считать, что игрок А — это заяц, игрок В — контролер.

У зайца 2 стратегии:

А₁ – не покупать билет

А₂ – купить билет

У контролера:

В₁ – не проверять наличие билета

В₂ – проверить

Цена билета – 300.000. Штраф — 5.000.000.

Платежная матрица:

	В1	В2
А1 А2	300000 300000	5000000 0

3). Игра “полковника Блотто”.

Две воюющие армии ведут борьбу за 2 населенных пункта. Армия полковника Б. состоит из 4 полков, армия противника из 3-х полков. Армия, которая посылает больше полков в том или иной населенный пункт, занимает его и уничтожают все силы противника. Она получает по единице за каждый занятый пункт и за каждый уничтоженный полк противника. Полковник Б. должен решить, как распределить свои полки, чтобы выиграть максимум количества очков. Очевидно, что у полковника Б. имеется 5 стратегии распределения своих сил. Каждую стратегии можно представить парой чисел (x,y), где х – число полков, посылаемых и 1 –й населенный пункт, у- во 2-й. Аналогично представлены стратегии противника, их 4. Определить стратегии полковника Б. и его противника и платежную матрицу.

Выводы:

Игрой наз. Модель конфликтных ситуации, в которой определены набор стратегии каждого игрока и платежная матрица. В любой игре необходимо определить оптимальные стратегии ее участников, считая при этом, что каждый из игроков действует наилучшим для себя образом и при этом на глупость, просчеты своего противника не расчитыв. т.е. в основу теории игр положен так называемый принцип разумности противника. Т.е. математическая игра исключает возможность риска и любые случайные факторы, т.е. исключает то, что имеет место в реальности.

Игры с седловой точкой.

Рассмотрим игру двух игроков A и B с нулевой суммой. У игрока A — m частных стратегий A_i i=1,m.У игрока B — n частных стратегий B_j j=1,n.Платежная матрица C=( C_ij)_m?n . Матрица выигрышей игрока A задана в виде таблицы:

	B1	B2	—	Bn	min
A1	C11	C12	—	C1n	a1=min C1j
A2	C21	C22	—	C2n	a2=min C2j
—	—	—	—	—	—
Am	Am1	Cm2	—	Cij	am=min Cmj
—	—	—	—	—
max	B1=max Ci1	B2=max Ci2	—	Bn=max Cij

Игрок A выигрывающий и он стремится максимизировать свой выигрыш. Свою оптимальную стратегию он выбирает таким образом, чтобы игрок B никакими своими действиями не мог уменьшить выигрыш игрока A. Если игрок A выбирает стратегию A_i , то ему гарантирован выигрыш a_i=min C_ij , которой игрок B никакими своими действиями изменить не можеттак как это минимально возможный выигрыш игрока A при использовании стратегии A_i . Определим значения минимальных выигрышей для каждой из своих стратегий т.е. свою оптимальную стратегию игрок A выбирает по правилу:

max a_i=max min C_ij=a.

a называется нижней ценой игры, а соответствующая стратегия игрока A называется максимальной. Игрок B рассуждает аналогично.выбирая свою стратегию B_j , он определяет при этом гарантированный наибольший проигрыш, который игрок A никак своими действиями увеличить не сможет, т.е. для каждого столбца таблицы находят B_j=max C_ij , а затем среди B_j игрок B выбирает min, т.е. свою оптимальную стратегию игрок B выбирает по правилу:

min B_j=min max C_ij=b.

Число b называется верхней ценой игры. Стратегия игрока B, соответствующая b, называется минимаксной стратегией. Пара стратегий игроков максимальная и минимальная называют минимаксными стратегиями. Можно доказать, что

b?a , min max C_ij?max min C_ij

Если b=a, то max min C_ij= min max C_ij=С_i0j0=V. В этом случае оптимальные стратегии игроков A и B будут: A_i0 и B_j0, котороые соотвутствуют числу С_i0j0. В этом случае говорят, что игра имеет седловую точку и пара соответствующих стратегий (A_i0,B_j0) устанавливают ситуацию равновесия в игре. Выигрыш игрока A равен V= С_i0j0 ,V – цена игры. Если игра имеет седловую точку, то она является одноходовой и решение игры существует в чистых стратегиях.

Игры без седловых точек.

Рассмотрим игру “заяц — контролер”

	B1	B2	ai
A1 A2 bj	300 тыс. -300 тыс. 300 тыс.	-5 млн. 0 0	-5 млн. -300 тыс. a=-300 тыс. b=0

a?b ?седловой точки нет.

Максимальная стратегия игрока A – A₂.

Минимальная стратегия игрока B – B₂.

Рассмотрим другой пример:

	B1	B2	ai
A1 A2 bj	3 1 b1=3	-1 5 b2=5	a1= -1 a2 = 1 a=1 b=3

a?b

Максимальная стратегия игр A–A₂ гарантирует ему «максимально» возможный выигрыш , а минимальная стратегия игр B–B₂ гарантирует ему «минимально» возможный проигрыш что в такой ситуации игрок A хочет выигрыш больше, чем 1, что не противоречит………… пределах желанию игрока B проиграть меньше, чем 3. Игра седловой точки не имеет решения в чистых стратегиях нет, игра не является одноходовой. Следовотельно, для того, чтобы улучшить свои результаты, каждый из игроков должен применить свои чистые стратегии попеременно с определенной частотой, т.е. смешанные стратегии, которые имеют смысл при многоходовой игре.

Смешанные стратегии

Рассмотрим игру двух лиц А и В, заданную путем матрицы.

	B1	B2	—	Bn	min Cij
A1	C11	C12	—	C1n
A2	C21	C22	—	C2n
—	—	—	—	—
Am	Am1	Cm2	—	Cmn
max

Смешанные стратегии игроков будем искать в виде:

и — частоты, с которыми игроки А и В применяют свои чистые стратегии и . Тогда средний выигрыш игрока А будет определяться как МО:

Цель игрока А – максимальное увеличение своего выигрыша за счет применения своей смешанной стратегии при наилучшей игре игрока В – уменьшение своего проигрыша за счет своей смешанной стратегии при наилучшей игре игрока А. Для решения игры необходимо найти такие смешанные стратегии и , для которых будут выполнятся условия: