В ИУС обычно выдают 2 класса технологических процессов: непрерывные и дискретные, которые значительно отличаются между собой по способам описания, программирования, выполнения в режиме реального времени. К непрерывным процессам, например можно отнести управление станками ЧПУ, контурными работами, решение задач навигационного управления и т.д. В качестве примера непрерывного управления рассмотрим прямое цифровое регулирование.
При цифровом регулировании ЭВМ моделирует работу нескольких регуляторов. Каждая функция регулятора моделируется управляющей ЭВМ последовательно во времени.
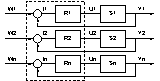
Структурная схема прямого цифрового регулятора.
Управляющая ИУС выдает на каждый контур в режиме прямого цифрового управления сигнал управления Uk (абсолютное значение) или его приращение ?Uk= Uk— Uk-1 (значение приращения). При выдаче управляющих сигналов выполняется 2 задачи:
1) преобразование информационных сигналов в аналоговые для исполнительного звена
2) фиксация аналогового сигнала до появления нового значения.
При выдаче абсолютных значений параметров процесса функция фиксации осуществляется выходными регистрами модулей УАП. При задании значений приращения функцию фиксации можно осуществлять вне ЭВМ специальным интегр-м исполнительным звеном (двигателем, шагов. двигателем).
Рассмотрим реализацию приведенных зависимостей на примере ПИД-алгоритма (пропорц.-интегрально дифференциальный) в последов. схеме регулятор – исполнит. механизм. Между отклонения от сигнала регулирования e(t) и управляющим сигналом Y(t) существует зависимость:
При цифровой реализации приведенной зависимости дифференциальное управление преобразовывается в разностное, т.к. непрерывные функции времени e(t) и Y(t) определяются своими значениями en, en-1, Yn, Yn-1 только в моменты опроса КТА (ТА – период опроса) К=0,1,…,n.
Т.о. набору значений управляющих сигналов Yn ставиться в соответствие последовательность значений отклонения регулирования en. Интеграл и производная в управлении апроксимируются соответственно суммой членов и разностью.