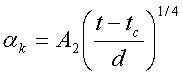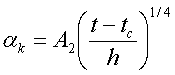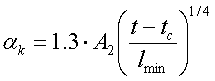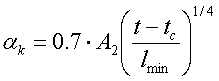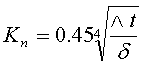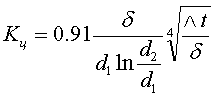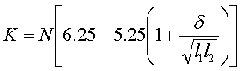А) Тонкие стержни (провода).
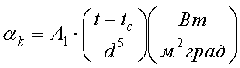— Коэффициент конвективного теплообмена.
d – диаметр провода, А – из таблицы:
|
Среда |
Значение А1 при температуре tm. |
||||||
|
0 |
20 |
40 |
60 |
80 |
100 |
120 |
|
|
Воздух Вода |
0,291 9,35 |
0,295 13,1 |
0,3 15,7 |
0,306 17,6 |
0,310 19,0 |
0,315 20 |
0,320 ——— |
Б) Если определяющий размер L плоской или цилиндрической поверхности и ее температурный набор (t-tc) удовлетворяют неравенству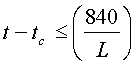 
, то движение жидкости подчиняется закону степени ?. В противном случае имеет место теплообмен по закону степени 1/3.
|
Рассматриваемое тело |
Закон степени 1/4 |
Закон степени 1/3 |
|
Шары, горизонтальные цилиндры с радиусом d. |
|
|
|
Вертикальные пластины и цилиндры с высотой h. |
|
|
|
Горизонтальная пластина, рассеивающая тепловой поток вверх (lmin – наименьший размер пластины) |
|
|
|
Горизонтальная пластина, рассеивающая тепловой поток вниз. |
|
|
![clip_image008[1]](http://studentpmr.ru/wp-content/uploads/2009/04/clip-image008114.gif "clip_image008[1]"){kind=small}
|
Среда |
Значение А2 при температуре tm. |
|||||||||
|
10 |
20 |
30 |
40 |
60 |
80 |
100 |
120 |
140 |
150 |
|
|
Воздух Вода |
1.4 90 |
1.38 105 |
1.36 127 |
1.34 149 |
1.31 178 |
1.29 208 |
1.27 227 |
1.26 — |
1.25 — |
1.245 — |
|
Среда |
Значение А3 при температуре tm. |
||||||
|
0 |
20 |
40 |
60 |
80 |
100 |
150 |
|
|
Воздух Вода |
1.69 102 |
1.61 198 |
1.53 290 |
1.45 363 |
1.39 425 |
1.33 480 |
1.23 610 |
Выражение для коэффициентов теплопередачи К через плоскую и цилиндрическую прослойку, заполненную воздухом принимает вид:
В) Конвективная теплопередача внутри ограниченного объема, имеющего форму параллелепипеда, одна грань которого имеет температуру t1, все остальные грани имеют температуру t2. Причем t1 > t2. Коэффициент конвективно – кондуктивной теплопередачи через такую прослойку, заполненную воздухом, находится по формуле:
, где
l1 и l2 – длина и ширина нагретой грани, ? – толщина прослойки. N- коэффициент, учитывающий ориентацию в пространстве нагретой грани (Nв=1 – вертикальное расположение; Nг=1,3 — горизонтальное).
Коэффициент А5 зависит от температуры 
.
|
tm |
0 |
50 |
100 |
200 |
|
A5 |
0.63 |
0.58 |
0.56 |
0.44 |
Задача №1.
Определить среднеповерхностную температуру герметичного корпуса, если задано: L1, L2, h, P*, ?k, tc.
Решение:
1) Задаем температуру корпуса аппарата: 
.
2) Определим 
Т.к. среда не ограничена и все поверхности ограничены одинаково, то 
